
(本小题满分13分)设数列 的前项和为
的前项和为 ,且
,且
 ,
, 为等差数列,且
为等差数列,且 ,
, .
.
(Ⅰ)求数列 和
和 通项公式;
通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和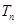 .
.
(1)当 时,
时, .…………1分
.…………1分
当 时,
时, ,…………3分
,…………3分
此式对 也成立.
也成立. 
 .………………………4分 ,
.………………………4分 ,
从而 ,
, .又因为
.又因为 为等差数列,
为等差数列, 公差
公差 ,……………………………………………………………… 5分
,……………………………………………………………… 5分 .………………………………………………6分
.………………………………………………6分
(2)由(1)可知 ,…………………………7分
,…………………………7分
所以 .①
.① .②……9分
.②……9分
①-②得:


 .………………………………………………12分
.………………………………………………12分 .…………………………………………………13分
.…………………………………………………13分
解析试题分析:(Ⅰ)由an=  可求数列{an}的通项公式,进而可求数列{bn}通项公式;
可求数列{an}的通项公式,进而可求数列{bn}通项公式;
(Ⅱ)由(Ⅰ)可知cn=(2n-1)•2n-1,故可用错位相减法来求数列的前n项和.
考点:本试题主要考查了数列的求通项和求和的综合应用,涉及等差等比数列以及错位相减法求和,属中档题。
点评:解决该试题的易错点是错位相减法的准确求解,尤其是项数的确定问题。


科目:高中数学 来源: 题型:解答题
已知等差数列{an}的首项a1=1,公差d>0,且第2项,第5项,第14项分别是等比数列{bn}的第2项,第3项,第4项.
(1)求数列{an}与{bn}的通项公式;
(2)求数列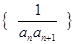 的前n项和
的前n项和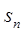
(3)设数列{cn}对任意自然数n,均有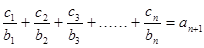 ,求c1+c2+c3+……+c2006值.
,求c1+c2+c3+……+c2006值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知{an}为等差数列,且a3=-6,a6=0.
(1)求{an}的通项公式;
(2)若等比数列{bn}满足b1=-8,b2=a1+a2+a3,求{bn}的前n项和公式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com