
【题目】进入21世纪以来,南康区家具产业快速发展,为广大市民提供了数十万就业岗位,提高了广大市民的收入,也带动南康和周边县市的经济快速发展.同时,由于生产设备相对落后,生产过程中产生大量粉尘、废气,给人们的健康、交通安全等带来了严重影响.经研究发现,工业废气、粉尘等污染物排放是雾霾形成和持续的重要原因,治理污染刻不容缓.为此,某工厂新购置并安装了先进的废气、粉尘处理设备,使产生的废气、粉尘经过过滤后再排放,以降低对空气的污染.已知过滤过程中废气粉尘污染物的数量![]() (单位:
(单位:![]() )与过滤时间
)与过滤时间![]() (单位:
(单位:![]() )间的关系为
)间的关系为![]()
![]() (
(![]() 均为非零常数,
均为非零常数,![]() 为自然对数的底数)其中
为自然对数的底数)其中![]() 为
为![]() 时的污染物数量.若过滤
时的污染物数量.若过滤![]() 后还剩余
后还剩余![]() 的污染物.
的污染物.
(1)求常数![]() 的值.
的值.
(2)试计算污染物减少到![]() 至少需要多长时间(精确到
至少需要多长时间(精确到![]() .参考数据:
.参考数据:![]() )
)
科目:高中数学 来源: 题型:
【题目】假定生男孩和生女孩是等可能的,令![]() {一个家庭中既有男孩又有女孩},
{一个家庭中既有男孩又有女孩},![]() {一个家庭中最多有一个女孩}.对下述两种情形,讨论
{一个家庭中最多有一个女孩}.对下述两种情形,讨论![]() 与
与![]() 的独立性.
的独立性.
(1)家庭中有两个小孩;
(2)家庭中有三个小孩.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中,
中,![]() ,且
,且![]() 对任意正整数
对任意正整数![]() 都成立,数列
都成立,数列![]() 的前
的前![]() 项和为
项和为![]() .
.
(1)若![]() ,且
,且![]() ,求
,求![]() ;
;
(2)是否存在实数k,使数列![]() 是公比不为1的等比数列,且任意相邻三项
是公比不为1的等比数列,且任意相邻三项![]() 按某顺序排列后成等差数列,若存在,求出所有k的值;若不存在,请说明理由;
按某顺序排列后成等差数列,若存在,求出所有k的值;若不存在,请说明理由;
(3)若![]() ,求
,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为迎接![]() 年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了
年北京冬季奥运会,普及冬奥知识,某校开展了“冰雪答题王”冬奥知识竞赛活动.现从参加冬奥知识竞赛活动的学生中随机抽取了![]() 名学生,将他们的比赛成绩(满分为
名学生,将他们的比赛成绩(满分为![]() 分)分为
分)分为![]() 组:
组:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.

(Ⅰ)求![]() 的值;
的值;
(Ⅱ)记![]() 表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于
表示事件“从参加冬奥知识竞赛活动的学生中随机抽取一名学生,该学生的比赛成绩不低于![]() 分”,估计
分”,估计![]() 的概率;
的概率;
(Ⅲ)在抽取的![]() 名学生中,规定:比赛成绩不低于
名学生中,规定:比赛成绩不低于![]() 分为“优秀”,比赛成绩低于
分为“优秀”,比赛成绩低于![]() 分为“非优秀”.请将下面的
分为“非优秀”.请将下面的![]() 列联表补充完整,并判断是否有
列联表补充完整,并判断是否有![]() 的把握认为“比赛成绩是否优秀与性别有关”?
的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 |
| ||
女生 |
| ||
合计 |
|
参考公式及数据:![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中央政府为了应对因人口老龄化而造成的劳动力短缺等问题,拟定出台“延迟退休年龄政策”.为了了解人们]对“延迟退休年龄政策”的态度,责成人社部进行调研.人社部从网上年龄在15![]() 65岁的人群中随机调查100人,调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
65岁的人群中随机调查100人,调査数据的频率分布直方图和支持“延迟退休”的人数与年龄的统计结果如下:
年龄 |
|
|
|
|
|
支持“延迟退休”的人数 | 15 | 5 | 15 | 28 | 17 |
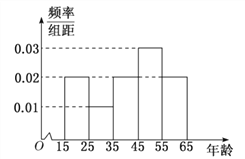
(1)由以上统计数据填![]() 列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
列联表,并判断能否在犯错误的概率不超过0.05的前提下认为以45岁为分界点的不同人群对“延迟退休年龄政策”的支持度有差异;
45岁以下 | 45岁以上 | 总计 | |
支持 | |||
不支持 | /td> | ||
总计 |
(2)若以45岁为分界点,从不支持“延迟退休”的人中按分层抽样的方法抽取8人参加某项活动.现从这8人中随机抽2人
①抽到1人是45岁以下时,求抽到的另一人是45岁以上的概率.
②记抽到45岁以上的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班50位学生期中考试数学成绩的频率分布直方图如图所示,其中成绩分组区间是:[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]
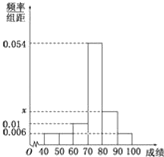
(Ⅰ)求图中![]() 的值,并估计该班期中考试数学成绩的众数;
的值,并估计该班期中考试数学成绩的众数;
(Ⅱ)从成绩不低于90分的学生和成绩低于50分的学生中随机选取2人,求这2人成绩均不低于90分的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某县共有90间农村淘宝服务站,随机抽取5间,统计元旦期间的网购金额(单位:万元)的茎叶图如图所示,其中茎为十位数,叶为个位数.
(1)根据茎叶图计算样本均值;
(2)若网购金额(单位:万元)不小于18的服务站定义为优秀服务站,其余为非优秀服务站.根据茎叶图推断90间服务站中有几间优秀服务站?
(3)从随机抽取的5间服务站中再任取2间作网购商品的调查,求恰有1间是优秀服务站的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为制定合理的节电方案,对居民用电情况进行了调查,通过抽样,获得了某年200户居民每户的月均用电量(单位:百度),将数据按照![]() ,
,![]() ,
,![]() 分成
分成![]() 组,制成了如图所示的频率分布直方图:
组,制成了如图所示的频率分布直方图:

(I)求直方图中![]() 的值;
的值;
56789月均用电量百厦
(Ⅱ)设该市有100万户居民,估计全市每户居民中月均用电量不低于6百度的人数,估计每户居民月均用电量的中位数,说明理由;
(Ⅲ)政府计划对月均用电量在4(百度)以下的用户进行奖励,月均用电量在![]() 内的用户奖励20元/月,月均用电量在
内的用户奖励20元/月,月均用电量在![]() 内的用户奖励10元/月,月均用电量在
内的用户奖励10元/月,月均用电量在![]() 内的用户奖励2元/月.若该市共有400万户居民,试估计政府执行此计划的年度预算.
内的用户奖励2元/月.若该市共有400万户居民,试估计政府执行此计划的年度预算.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com