
分析 (Ⅰ)利用数列递推式,结合等比数列的定义,即可得到结论;
(Ⅱ)方法一:利用放缩法证明.
方法二:用数学归纳法证明.
解答 证明:(Ⅰ)由an+1=2an+2,得an+1+2=2(an+2),
即$\frac{{{a_n}_{+1}+2}}{{{a_n}+2}}=2$,
所以,数列{an+2}是公比为2的等比数列.${a_n}+2=({{a_1}+2})•{2^{n-1}}={2^{n+1}}$,
所以${a_n}={2^{n+1}}-2$.
(Ⅱ)法一:$\frac{1}{a_n}=\frac{1}{{{2^{n+1}}-2}}≤\frac{1}{2^n}$(当n=1时取“=”),
所以$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{a_n}$$≤\frac{1}{2^1}+\frac{1}{2^2}+…+\frac{1}{2^n}$=$\frac{{\frac{1}{2}(1-\frac{1}{2^n})}}{{1-\frac{1}{2}}}=1-\frac{1}{2^n}$.
法二:用数学归纳法.
(1)当n=1时,$\frac{1}{a_1}=\frac{1}{2},1-\frac{1}{2^1}=\frac{1}{2}$,原不等式成立.
(2)假设当n=k(k≥1,k∈N*)时,不等式成立,即$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{a_k}≤1-\frac{1}{2^k}$,
则当n=k+1时,$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{a_k}+\frac{1}{{{a_{k+1}}}}$$≤({1-\frac{1}{2^k}})+\frac{1}{{{2^{k+2}}-2}}$=$1-\frac{{3•{2^k}-2}}{{{2^k}•({{2^{k+2}}-2})}}$=$1-\frac{1}{{{2^{k+1}}}}•\frac{{({{2^k}-1})+({{2^{k+1}}-1})}}{{{2^{k+1}}-1}}$$≤1-\frac{1}{{{2^{k+1}}}}$
这说明,当n=k+1时,原不等式也成立.
综合(1)(2),可知:$\frac{1}{a_1}+\frac{1}{a_2}+…+\frac{1}{a_n}≤1-\frac{1}{2^n}$,n∈N*.
点评 本题考查等比数列的证明以及不等式的证明,考查学生的计算能力和转化能力,属于中档题


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:选择题
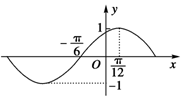
| A. | $y=sin(x+\frac{π}{6})$ | B. | $y=sin(2x-\frac{π}{6})$ | C. | $y=sin(2x+\frac{π}{6})$ | D. | $y=sin(2x+\frac{π}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,$∠ABC=\frac{π}{3}$,且PA⊥平面ABCD.
如图,四棱锥P-ABCD,底面ABCD是边长为2的菱形,$∠ABC=\frac{π}{3}$,且PA⊥平面ABCD.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,x+1>ex | B. | ?x∈R,x+1≥ex | C. | ?x∈R,x+1≥ex | D. | ?x∈R,x+1>ex |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}+1}}{4}$ | B. | $\frac{{\sqrt{3}-1}}{2}$ | C. | $\frac{{3-\sqrt{3}}}{4}$ | D. | $\frac{{3-\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{26}{5}$ | B. | -$\frac{26}{5}$ | C. | ±$\frac{26}{5}$ | D. | -$\frac{5}{26}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com