
| A. | $\frac{2\sqrt{3}}{3}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{6}}{2}$ | D. | 1 |
分析 不妨设定点O(0,0),M(0,y),P(a,0),Q(x,y-b),B(x,y),由(x-a)2+(y-b)2=x2+b2=y2+a2.得|PM|=|PQ|=|MQ|,可得:△MPQ是等边三角形.不妨设∠OMP=θ,$(0≤θ≤\frac{π}{6})$,∠BMQ=$\frac{π}{6}$-θ,可得:$\frac{x}{y}$=$\frac{|BM|}{|OM|}$=$\frac{|BM|}{|MQ|}•\frac{|PM|}{|OM|}$=$\frac{cos(\frac{π}{6}-θ)}{cosθ}$=$\frac{\sqrt{3}}{2}$+$\frac{tanθ}{2}$,即可得出.
解答 解:不妨设定点O(0,0),M(0,y),P(a,0),Q(x,y-b),B(x,y),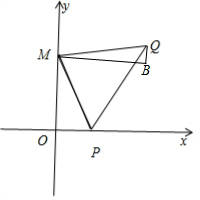
由(x-a)2+(y-b)2=x2+b2=y2+a2.得|PM|=|PQ|=|MQ|,
∴△MPQ是等边三角形.
不妨设∠OMP=θ,$(0≤θ≤\frac{π}{6})$,则∠BMQ=$\frac{π}{6}$-θ,
∴$\frac{x}{y}$=$\frac{|BM|}{|OM|}$=$\frac{|BM|}{|MQ|}•\frac{|PM|}{|OM|}$=$\frac{cos(\frac{π}{6}-θ)}{cosθ}$=$\frac{\sqrt{3}}{2}$+$\frac{tanθ}{2}$≤$\frac{\sqrt{3}}{2}$+$\frac{tan\frac{π}{6}}{2}$=$\frac{2\sqrt{3}}{3}$,
当且仅当θ=$\frac{π}{6}$时取等号.
故选:A.
点评 本题考查了等边三角形的性质、圆的方程、三角函数求值,考查了推理能力与计算能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{3}{2}i$ | B. | $\frac{1}{2}i$ | C. | $-\frac{3}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
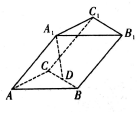 如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )
如图,在三棱柱ABC-A1B1C1中,底面ABC是边长为2的等边三角形,点A1在底面ABC上的投影D恰好为BC的中点,AA1与平面ABC所成角为45°,则该三棱柱的体积为( )| A. | 1 | B. | $\sqrt{2}$ | C. | 3 | D. | $\sqrt{10}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 超市 | A | B | C | D | E | F | G |
| 广告费支出xi | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
| 销售额yi | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com