
| A. | $\frac{{\sqrt{3}+1}}{4}$ | B. | $\frac{{\sqrt{3}-1}}{2}$ | C. | $\frac{{3-\sqrt{3}}}{4}$ | D. | $\frac{{3-\sqrt{3}}}{2}$ |
分析 由题意,首先找出满足条件的x,y的约束条件,并画出区域,利用面积比求概率.
解答  解:由题意,x,y满足$\left\{\begin{array}{l}1+{x^2}>y\\ 1+y>{x^2}\\{x^2}+y>1\end{array}\right.$,作出可行域如下,${S_阴}=\int_0^1{[{({{x^2}+1})-({1-{x^2}})}]}dx+\int_1^{\sqrt{3}}{[{2-({{x^2}-1})}]}dx$=$\frac{2}{3}{x^3}\left|\begin{array}{l}1\\ 0\end{array}\right.+(3x-\frac{1}{3}{x^3})\left|\begin{array}{l}\sqrt{3}\\ 1\end{array}\right.=2\sqrt{3}-2$,
解:由题意,x,y满足$\left\{\begin{array}{l}1+{x^2}>y\\ 1+y>{x^2}\\{x^2}+y>1\end{array}\right.$,作出可行域如下,${S_阴}=\int_0^1{[{({{x^2}+1})-({1-{x^2}})}]}dx+\int_1^{\sqrt{3}}{[{2-({{x^2}-1})}]}dx$=$\frac{2}{3}{x^3}\left|\begin{array}{l}1\\ 0\end{array}\right.+(3x-\frac{1}{3}{x^3})\left|\begin{array}{l}\sqrt{3}\\ 1\end{array}\right.=2\sqrt{3}-2$,
由几何概型的公式得到$p=\frac{{2\sqrt{3}-2}}{2×2}=\frac{{\sqrt{3}-1}}{2}$;
故选:B.
点评 本题考查了几何概型的概率求法;关键是明确事件的几何测度为面积,所以用面积比求概率是事件中两个变量时经常选择的方法.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | ① | B. | ② | C. | ③ | D. | ①或③ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0.35 | B. | 0.32 | C. | 0.55 | D. | 0.68 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{30}}}{6}$ | B. | $\frac{2}{3}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 变量x | 2.7 | 2.9 | 3 | 3.2 | 4.2 |
| 变量y | 46 | 49 | m | 53 | 55 |
| A. | 50 | B. | 51 | C. | 52 | D. | 53 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
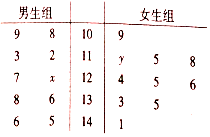 在某小学体育素质达标运动会上,对10名男生和10名女生在一分钟跳绳的次数进行统计,得到如下所示茎叶图:
在某小学体育素质达标运动会上,对10名男生和10名女生在一分钟跳绳的次数进行统计,得到如下所示茎叶图:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com