
【题目】已知函数![]()
(1)当![]() 时,求曲线y=f(x)在点(1,f(1))处的切线方程;(2)求函数
时,求曲线y=f(x)在点(1,f(1))处的切线方程;(2)求函数![]() 的单调区间和极值
的单调区间和极值
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
(1)把a=1代入原函数解析式中,求出函数在x=1时的导数值,直接利用直线方程的点斜式写直线方程;
(2)求出函数的导函数,由导函数可知,当a≤0时,f′(x)>0,函数在定义域(0,+∝)上单调递增,函数无极值,当a>0时,求出导函数的零点,由导函数的零点对定义域分段,利用原函数的单调性得到函数的极值.
(1)当![]() 时
时![]() ,则
,则
![]() ,所以
,所以![]() ,
,
又![]()
所以曲线![]() 在
在![]() 处的切线方程为
处的切线方程为![]() ,
,
即![]()
(2)由![]() 得
得![]() .
.
①当![]() 时,
时,![]() ,函数
,函数![]() 在
在![]() 上单调递增,函数无极大值,也无极小值;
上单调递增,函数无极大值,也无极小值;
②当![]() 时,由
时,由![]() 得
得![]() 或
或![]() (舍负),于是当
(舍负),于是当![]() 时、
时、![]() 在
在![]() 上单调递减;当
上单调递减;当![]() 时,
时,![]() 在
在![]() 上单调递增,函数
上单调递增,函数![]() 在
在![]() 处取得极小值
处取得极小值![]() ,无极大值.
,无极大值.
综上所述:
当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ,函数
,函数![]() 既无极大值也无极小值;
既无极大值也无极小值;
当a>0时,函数![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() ,函数
,函数![]() 有极小值
有极小值![]() ,无极大值
,无极大值


科目:高中数学 来源: 题型:
【题目】如图在△AOB中,∠AOB=90°,AO=2,OB=1,△AOC可以通过△AOB以直线AO为轴旋转得到,且OB⊥OC,点D为斜边AB的中点.
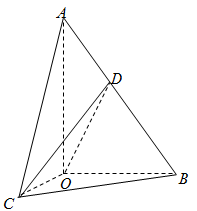
(1)求异面直线OB与CD所成角的余弦值;
(2)求直线OB与平面COD所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》中,将底面为长方形且有一条侧棱与地面垂直的四棱锥称之为阳马,将四个面都为直角三角形的四面体称之为鳖臑,首届中国国际进口博览会的某展馆棚顶一角的钢结构可以抽象为空间图形阳马,如图所示,在阳马![]() 中,
中,![]() 底面
底面![]() .
.
(1)已知![]() ,斜梁
,斜梁![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求立柱
,求立柱![]() 的长;(精确到
的长;(精确到![]() )
)
(2)求证:四面体![]() 为鳖臑.
为鳖臑.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】化简
(1)![]()
(2)![]()
【答案】(1) ![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)切化弦可得三角函数式的值为-1
(2)结合三角函数的性质可得三角函数式的值为![]()
试题解析:
(1)tan70°cos10°( ![]() tan20°﹣1)
tan20°﹣1)
=cot20°cos10°( ![]() ﹣1)
﹣1)
=cot20°cos10°(![]() )
)
=![]() ×cos10°×(
×cos10°×(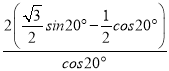 )
)
=![]() ×cos10°×(
×cos10°×(![]() )
)
=![]() ×(﹣
×(﹣![]() )
)
=﹣1
(2)∵(1+tan1°)(1+tan44°)=1+(tan1°+tan44°)+tan1°tan44°
=1+tan(1°+44°)[1﹣tan1°tan44°]+tan1°tan44°=2.
同理可得(1+tan2°)(1+tan43°)
=(1+tan3°)(1+tan42°)
=(1+tan4°)(1+tan41°)=…=2,
故![]() =
=![]()
点睛:三角函数式的化简要遵循“三看”原则:一看角,这是重要一环,通过看角之间的差别与联系,把角进行合理的拆分,从而正确使用公式 ;二看函数名称,看函数名称之间的差异,从而确定使用的公式,常见的有切化弦;三看结构特征,分析结构特征,可以帮助我们找到变形的方向,如遇到分式要通分等.
【题型】解答题
【结束】
18
【题目】平面内给定三个向量![]()
(1)求![]()
(2)求满足![]() 的实数
的实数![]() .
.
(3)若![]() ,求实数
,求实数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某汽车生产厂家为了解某型号电动汽车的“实际平均续航里程数”,收集了使用该型号电动汽车![]() 年以上的部分客户的相关数据,得到他们的电动汽车的“实际平均续航里程数”.从年龄在40岁以下的客户中抽取10位归为A组,从年龄在40岁(含40岁)以上的客户中抽取10位归为B组,将他们的电动汽车的“实际平均续航里程数”整理成下图,其中“+”表示A组的客户,“⊙”表示B组的客户.
年以上的部分客户的相关数据,得到他们的电动汽车的“实际平均续航里程数”.从年龄在40岁以下的客户中抽取10位归为A组,从年龄在40岁(含40岁)以上的客户中抽取10位归为B组,将他们的电动汽车的“实际平均续航里程数”整理成下图,其中“+”表示A组的客户,“⊙”表示B组的客户.
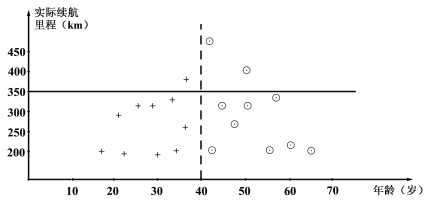
注:“实际平均续航里程数”是指电动汽车的行驶总里程与充电次数的比值.
(Ⅰ)记A,B两组客户的电动汽车的“实际平均续航里程数”的平均值分别为![]() ,
,![]() ,根据图中数据,试比较
,根据图中数据,试比较![]() ,
,![]() 的大小(结论不要求证明);
的大小(结论不要求证明);
(Ⅱ)从A,B两组客户中随机抽取2位,求其中至少有一位是A组的客户的概率;
(III)如果客户的电动汽车的“实际平均续航里程数”不小于350,那么称该客户为“驾驶达人”.从A,B两组客户中,各随机抽取1位,记“驾驶达人”的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及其数学期望
的分布列及其数学期望![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 中
中![]() ,函数
,函数![]() .
.
(1)若正项数列![]() 满足
满足![]() ,试求出
,试求出![]() ,
, ![]() ,
, ![]() ,由此归纳出通项
,由此归纳出通项![]() ,并加以证明;
,并加以证明;
(2)若正项数列![]() 满足
满足![]() (n∈N*),数列
(n∈N*),数列![]() 的前项和为Tn,且
的前项和为Tn,且![]() ,求证:
,求证: ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com