
分析 欲求所投的点落在阴影内部的概率,利用几何概型解决,只须利用定积分求出阴影图的面积,最后利用它们的面积比求得即可概率.
解答 解:由定积分可求得阴影部分图形Ω的面积为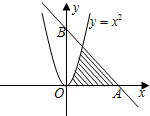 :
:
S=∫02x2dx+∫26(6-x)dx
=$\frac{1}{3}{x}^{3}{|}_{0}^{2}+(6x-\frac{1}{2}{x}^{2}){|}_{2}^{6}$=$\frac{32}{3}$,
又Rt△AOB的面积为:$\frac{1}{2}×6×6$=18
所以P=$\frac{\frac{32}{3}}{18}$=$\frac{16}{27}$.
故答案为:$\frac{16}{27}$.
点评 本题考查了利用定积分求面积以及几何摡型知识,考查运算求解能力,考查数形结合思想、化归与转化思想.属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -$\frac{2}{3}$ | C. | -$\frac{12}{5}$ | D. | $\frac{\sqrt{2}-4}{7}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
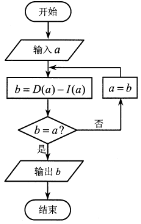 设a是一个各位数字都不是0且没有重复数字的三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a),(例如a=746,
设a是一个各位数字都不是0且没有重复数字的三位数,将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a),(例如a=746,查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=f(x+π) | B. | f(x)=f(x+$\frac{π}{2}$) | C. | f(x)=f($\frac{π}{3}$-x) | D. | f(x)=f($\frac{π}{6}$-x) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com