
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:填空题
已知正方体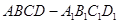 ,点
,点 、
、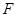 、
、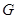 分别是棱
分别是棱 、
、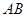 和
和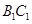 上的动点,观察直线
上的动点,观察直线 与
与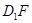 ,
, 与
与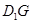 .
.
给出下列结论:
①对于任意点 ,存在点
,存在点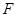 ,使得
,使得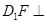
 ;②对于任意点
;②对于任意点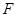 ,存在点
,存在点 ,使得
,使得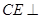
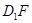 ;
;
③对于任意点 ,存在点
,存在点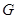 ,使得
,使得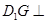
 ;④对于任意点
;④对于任意点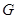 ,存在点
,存在点 ,使得
,使得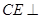
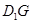 .
.
其中,所有正确结论的序号是__________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
过两平行平面α、β外的点P两条直线AB与CD,它们分别交α于A、C两点,交β于B、D两点,若PA=6,AC=9,PB=8,则BD的长为_______.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
设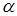 和
和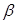 为不重合的两个平面,给出下列命题:
为不重合的两个平面,给出下列命题:
(1)若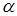 内的两条相交直线分别平行于
内的两条相交直线分别平行于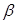 内的两条直线,则
内的两条直线,则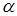 平行于
平行于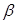 ;
;
(2)若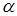 外一条直线
外一条直线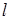 与
与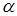 内的一条直线平行,则
内的一条直线平行,则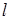 和
和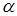 平行;
平行;
(3)设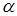 和
和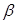 相交于直线
相交于直线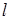 ,若
,若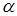 内有一条直线垂直于
内有一条直线垂直于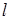 ,则
,则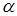 和
和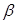 垂直;
垂直;
(4)直线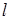 与
与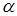 垂直的充分必要条件是
垂直的充分必要条件是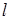 与
与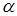 内的两条直线垂直.
内的两条直线垂直.
上面命题中,真命题的序号 (写出所有真命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知直线l⊥平面α,直线mÍ平面β,则下列四个命题:
①若α∥β,则l⊥m; ②若α⊥β,则l∥m;
③若l∥m,则α⊥β; ④若l⊥m,则α∥β.
其中正确命题的序号是
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
在平面几何里,有勾股定理:“设△ABC的两边AB,AC互相垂直,则AB2+AC2=BC2.”拓展到空间,类比平面几何的勾股定理,研究三棱锥的面面积与底面面积间的关系。可以得出的正确结论是:“设三棱锥A—BCD的三个侧面ABC、ACD、ADB两两相互垂直,则 ”.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知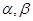 是两个互相垂直的平面,
是两个互相垂直的平面, 是一对异面直线,下列五个结论:
是一对异面直线,下列五个结论:
(1) ,
, (2)
(2)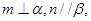 (3)
(3)
(4) (5)
(5) 。其中能得到
。其中能得到 的结论有 (把所有满足条件的序号都填上)
的结论有 (把所有满足条件的序号都填上)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com