
| 年份 | 2012 | 2013 | 2014 | 2015 | 2016 |
| 收入(万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
| 支出(万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
| A. | 11.4 | B. | 11.8 | C. | 12.0 | D. | 12.2 |
分析 由表中数据计算平均数$\overline{x}$、$\overline{y}$,
代入回归方程求出a,写出回归方程,
把x=15代入回归方程计算$\stackrel{∧}{y}$的值.
解答 解:由表中数据,计算$\overline{x}$=$\frac{1}{5}$×(8.2+8.6+10.0+11.3+11.9)=10,
$\overline{y}$=$\frac{1}{5}$×(6.2+7.5+8.0+8.5+9.8)=8,
代入回归方程可得a=8-0.76×10=0.4,
∴回归方程为$\stackrel{∧}{y}$=0.76x+0.4,
把x=15代入回归方程计算$\stackrel{∧}{y}$=0.76×15+0.4=11.8.
故选:B.
点评 本题考查了线性回归方程与平均值的计算问题,是基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
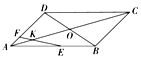 如图,平行四边形ABCD的两条对角线相交于点O,点E、F分别在边AB、AD上,$\overrightarrow{AE}$=$\frac{5}{7}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AD}$,直线EF交于AC于点K,$\overrightarrow{AK}$=λ$\overrightarrow{AO}$,则λ等于( )
如图,平行四边形ABCD的两条对角线相交于点O,点E、F分别在边AB、AD上,$\overrightarrow{AE}$=$\frac{5}{7}$$\overrightarrow{AB}$,$\overrightarrow{AF}$=$\frac{1}{4}$$\overrightarrow{AD}$,直线EF交于AC于点K,$\overrightarrow{AK}$=λ$\overrightarrow{AO}$,则λ等于( )| A. | $\frac{8}{27}$ | B. | $\frac{1}{3}$ | C. | $\frac{10}{27}$ | D. | $\frac{11}{27}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{5}-\frac{2}{5}$i | B. | $-\frac{1}{5}+\frac{2}{5}i$ | C. | $\frac{1}{5}+\frac{2}{5}$i | D. | $\frac{1}{5}-\frac{2}{5}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若命题p∧q为假命题,则p,q都是假命题 | |
| B. | 已知命题p:?x∈R,x2+x+1>0,则¬p:?x0∈R,x02+x0+1≤0 | |
| C. | 命题“若x2-3x+2=0,则x=1”的逆命题为:“若x≠1,则x2-3x+2≠0” | |
| D. | “x=1”是“x2-3x+2=0”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $2\sqrt{5}$ | B. | $\sqrt{5}$ | C. | $\frac{{\sqrt{10}}}{2}$ | D. | $\frac{{\sqrt{10}}}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -10 | B. | -13 | C. | -7 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分的中位数为me,众数为m0,平均值为$\overline x$,则( )
为了普及环保知识,增强环保意识,某大学随机抽取30名学生参加环保知识测试,得分(十分制)如图所示,假设得分的中位数为me,众数为m0,平均值为$\overline x$,则( )| A. | me=m0=$\overline x$ | B. | me=m0<$\overline x$ | C. | me<m0<$\overline x$ | D. | m0<me<$\overline x$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com