
分析 推导出f′(x)=Acos(x+θ)+$\frac{1}{2}sin(x-\frac{π}{6})$,由题设条件得:x∈[x1,x3]时,f′(x)有两个零点,由此能求出θ的值.
解答 解:∵f(x)=Asin(x+θ)-cos$\frac{x}{2}$cos($\frac{π}{6}$-$\frac{x}{2}$)(其中A为常数,θ∈(-π,0),
∴${f}^{'}(x)=Acos(x+θ)+\frac{1}{2}sin\frac{x}{2}cos(\frac{π}{6}-\frac{x}{2})$-$\frac{1}{2}cos\frac{x}{2}sin(\frac{π}{6}-\frac{x}{2})$
=Acos(x+θ)+$\frac{1}{2}sin(x-\frac{π}{6})$,
∵实数x1,x2,x3满足;①x1<x2<x3,②x3-x1<2π,③f(x1)=f(x2)=f(x3),
∴由题设条件①②③,得:x∈[x1,x3]时,f′(x)有两个零点,
当cos(x+θ)=ksin(x-$\frac{π}{6}$)时,f′(x)在[x1,x3]这个小于2π的区间才有两个零点,
即x+θ=x-$\frac{π}{6}$+$\frac{π}{2}$+kπ,
∵θ∈(-π,0),∴$θ=-\frac{π}{6}-\frac{π}{2}$=-$\frac{2π}{3}$.
故答案为:-$\frac{2π}{3}$.
点评 本题考查角的求法,是中档题,解题时要认真审题,注意导数性质和三角函数加法定理的合理运用.


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x}$ | B. | y=2|x| | C. | y=-log${\;}_{\frac{1}{2}}$x | D. | y=x|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
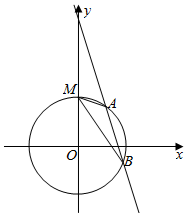 已知圆O:x2+y2=r2(r>0)与y轴的正半轴交于点M,直线l1:y=2x+1被圆O所截得的弦长为$\frac{4\sqrt{5}}{5}$,圆O上相异两动点A,B所在的直线l2的方程为y=kx+m,且满足直线MA与直线MB的斜率之积为$\frac{\sqrt{3}}{3}$.
已知圆O:x2+y2=r2(r>0)与y轴的正半轴交于点M,直线l1:y=2x+1被圆O所截得的弦长为$\frac{4\sqrt{5}}{5}$,圆O上相异两动点A,B所在的直线l2的方程为y=kx+m,且满足直线MA与直线MB的斜率之积为$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在下班高峰期,记者在某红绿灯路口随机访问10个步行下班的路人,其年龄的茎叶图如图:
在下班高峰期,记者在某红绿灯路口随机访问10个步行下班的路人,其年龄的茎叶图如图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com