
 在下班高峰期,记者在某红绿灯路口随机访问10个步行下班的路人,其年龄的茎叶图如图:
在下班高峰期,记者在某红绿灯路口随机访问10个步行下班的路人,其年龄的茎叶图如图:分析 (1)把茎叶图中的数据按照从小到大的顺序排列,求出中间两个数的平均数即是中位数;再求出这组数据的平均数与方差;
(2)40岁以上有7人,其中40~50岁有4人,50岁以上有3人,分别编号,用列举法求出从这7人中抽取2人的基本事件数以及一定含有50岁以上的基本事件数,计算对应的概率.
解答 解:(1)根据茎叶图中的数据,把这10个数据按照从小到大的顺序排列,
排在中间的两个数是43和45,则这组数据的中位数是$\frac{43+45}{2}$=44;
平均数是$\overline{x}$=$\frac{1}{10}$×(22+34+34+42+43+45+45+51+52+52)=42,
方差是s2=$\frac{1}{10}$[(22-42)2+(34-42)2×2+(42-42)2+(43-42)2
+(45-42)2×2+(51-42)2+(52-42)2×2=82.8;
(2)40岁以上的路人有7人,其中40~50岁有4人,记为a、b、c、d,
50岁以上有3人,记为E、F、G;
现从这7人中随机抽取2人,基本事件是
ab、ac、ad、aE、aF、aG、bc、bd、bE、bF、bG、cd、cE、
cF、cG、dE、dF、dG、EF、EG、FG共21种;
其中一定含有50岁以上的事件是aE、aF、aG、bE、bF、bG、cE、
cF、cG、dE、dF、dG、EF、EG、FG共15种;
所求的概率是P=$\frac{15}{21}$=$\frac{5}{7}$.
点评 本题考查了利用茎叶图中的数据求中位数与平均数、方差的应用问题,也考查了用列举法求古典概型的概率问题,是基础题目.


 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3} | B. | {1,3} | C. | {1,2} | D. | {1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 不存在x∈R,x2+x+1>0 | B. | 存在x0∈R,x02+x0+1>0 | ||
| C. | 存在x0∈R,x02+x0+1≤0 | D. | 对任意的x∈R,x2+x+1≤0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
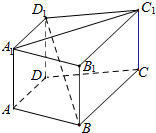 定义侧面与底面垂直的棱柱为直棱柱,在直四棱柱ABCD-A1B1C1D1中(如图),当底面四边形ABCD满足条件BD⊥AC时,有BD1⊥A1C1.
定义侧面与底面垂直的棱柱为直棱柱,在直四棱柱ABCD-A1B1C1D1中(如图),当底面四边形ABCD满足条件BD⊥AC时,有BD1⊥A1C1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com