
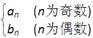 ,求数列{cn}的前101项之和T101;
,求数列{cn}的前101项之和T101; 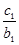 +
+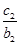 +…+
+…+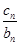 =an+1成立,求c1+c2+…+c2012的值.
=an+1成立,求c1+c2+…+c2012的值.
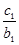 +
+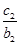 +…+
+…+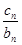 =an+1,求出{
=an+1,求出{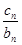 }的通项公式,然后根据通项公式的特点采用数列求和的方法求和即可.
}的通项公式,然后根据通项公式的特点采用数列求和的方法求和即可.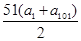 +
+
 …………………10分
…………………10分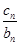 =
=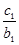 +
+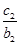 +…+
+…+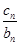 -(
-(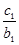 +
+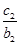 +…+
+…+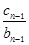 )=an+1-an=2
)=an+1-an=2 ……………………………13分
……………………………13分

 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com