
| A. | -3 | B. | 0 | C. | 6 | D. | 12 |
分析 由等差数列{an}(公差为d)的前n项和为Sn,则$\frac{{S}_{n}}{n}$=a1+$\frac{d}{2}$(n-1),可得数列$\{\frac{{S}_{n}}{n}\}$是等差数列,因此$\frac{d}{2}$=3,进而得出.
解答 解:由等差数列{an}(公差为d)的前n项和为Sn,则$\frac{{S}_{n}}{n}$=a1+$\frac{d}{2}$(n-1),
∴数列$\{\frac{{S}_{n}}{n}\}$是等差数列,
∴$\frac{d}{2}$=3,d=6
则a2016-a2014=2d=12.
故选:D.
点评 本题考查了等差数列的通项公式与求和公式及其性质,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{e}{2}$ | B. | 2 | C. | 1 | D. | $\frac{e}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某市乘坐出租车的收费办法如表:
某市乘坐出租车的收费办法如表:| (1)不超过4千米的里程收费12元; (2)超过4千米的里程按每千米2元收费(对于其中不足千米的部分,若其小于0.5千米则不收费,若其大于或等于0.5千米则按1千米收费); 当车程超过4千米时,另收燃油附加费1元. |
| A. | y=2[x+$\frac{1}{2}$]+4 | B. | y=2[x+$\frac{1}{2}$]+5 | C. | y=2[x-$\frac{1}{2}$]+4 | D. | y=2[x+$\frac{1}{2}$]+5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
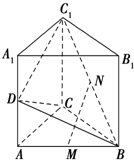 如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,AA1=4,D是棱AA1上的一点,M,N分别为BC1AB,的中点.
如图,已知直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=BC=2,AA1=4,D是棱AA1上的一点,M,N分别为BC1AB,的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-1)∪(0,1) | B. | (-∞,-1)∪(1,+∞) | C. | (-1,0)∪(1,+∞) | D. | (-1,0)∪(0,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com