Question

（13分）（2011•重庆）设α∈R，f（x）=cosx（asinx﹣cosx）+cos²（﹣x）满足，求函数f（x）在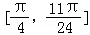上的最大值和最小值．

Answer 1

最大值是： 2  最小值为：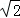

解析试题分析：利用二倍角公式化简函数f（x），然后，求出a的值，进一步化简为f（x）=2sin（2x﹣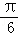），然后根据x的范围求出2x﹣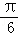，的范围，利用单调性求出函数的最大值和最小值．
解：f（x）=cosx（asinx﹣cosx）+cos²（﹣x）
=asinxcosx﹣cos²x+sin²x
=
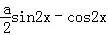
由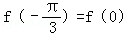得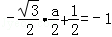
解得a=2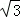
所以f（x）=2sin（2x﹣），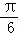
所以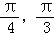x∈[]时2x﹣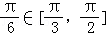，f（x）是增函数，
所以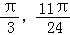x∈[]时2x﹣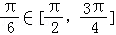，f（x）是减函数，
函数f（x）在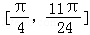上的最大值是：f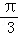（）=2；
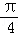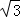又f（）=，f（）=；
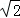所以函数f（x）在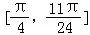上的最小值为：f（）=；
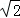点评：本题是中档题，考查三角函数的化简，二倍角公式的应用，三角函数的求值，函数的单调性、最值，考查计算能力，常考题型．