
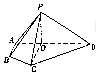
 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,O为为AD上的一点,且AB⊥AD,CO⊥AD,AB=AO=$\frac{1}{3}$AD=$\frac{1}{2}$OC=1,OP=$\frac{1}{2}$CD,PA=$\sqrt{3}$.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,O为为AD上的一点,且AB⊥AD,CO⊥AD,AB=AO=$\frac{1}{3}$AD=$\frac{1}{2}$OC=1,OP=$\frac{1}{2}$CD,PA=$\sqrt{3}$.分析 (1)由面面垂直的性质可得AB⊥AD,求解三角形证明PA⊥AD,再由线面垂直的判定可得PD⊥平面PAB;
(2)以O为坐标原点,建立如图所示空间直角坐标系,分别求出平面PAB与PBC的一个法向量,由两法向量所成角的余弦值可得平面PAB与平面PBC所成锐二面角的余弦值.
解答 (1)证明:如图,
∵平面PAD⊥平面ABCD,且平面PAD∩平面ABCD=AD,AB⊥AD,
∴AB⊥平面PAD,又PD?平面PAD,则AB⊥PD.
∵CO⊥AD,OC=2,OD=$\frac{2}{3}AD=2$,∴CD=$2\sqrt{2}$,
则OP=$\frac{1}{2}CD=\sqrt{2}$,
在△AOP中,AO2+OP2=1+2=3=PA2,
∴PO⊥AD,
在Rt△POD中,2PD2=OP2+OD2=2+4=6,
∵PA2+PD2=3+6=9=AD2,
∴PA⊥AD,
又PA∩AB=A,∴PD⊥平面PAB;
(2)解:以O为坐标原点,建立如图所示空间直角坐标系,
则P(0,0,$\sqrt{2}$),A(0,-1,0),B(1,-1,0),C(2,0,0),
∴$\overrightarrow{PA}=(0,-1,-\sqrt{2})$,$\overrightarrow{AB}=(1,0,0)$,$\overrightarrow{BC}=(1,1,0)$,$\overrightarrow{PC}=(2,0,-\sqrt{2})$.
分别设平面PAB与PBC的一个法向量为$\overrightarrow{m}=({x}_{1},{y}_{1},{z}_{1})$,$\overrightarrow{n}=({x}_{2},{y}_{2},{z}_{2})$.
由$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{PA}=-{y}_{1}-\sqrt{2}{z}_{1}=0}\\{\overrightarrow{m}•\overrightarrow{AB}={x}_{1}=0}\end{array}\right.$,取z1=1,得$\overrightarrow{m}=(0,-\sqrt{2},1)$;
由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{BC}={x}_{2}+{y}_{2}=0}\\{\overrightarrow{n}•\overrightarrow{PC}=2{x}_{2}-\sqrt{2}{z}_{2}=0}\end{array}\right.$,取${z}_{2}=\sqrt{2}$,得$\overrightarrow{n}=(1,-1,\sqrt{2})$.
∴cos<$\overrightarrow{m},\overrightarrow{n}$>=$\frac{\overrightarrow{m}•\overrightarrow{n}}{|\overrightarrow{m}||\overrightarrow{n}|}=\frac{2\sqrt{2}}{\sqrt{3}×2}=\frac{\sqrt{6}}{3}$.
∴平面PAB与平面PBC所成锐二面角的余弦值为-$\frac{\sqrt{6}}{3}$.
点评 本题考查线面垂直的判定,考查空间想象能力和思维能力,训练了利用空间向量求解二面角的平面角,是中档题.


 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示的多面体中,ABCD是平行四边形,BDEF是矩形,ED⊥面ABCD,∠ABD=$\frac{π}{6}$,AB=2AD.
如图所示的多面体中,ABCD是平行四边形,BDEF是矩形,ED⊥面ABCD,∠ABD=$\frac{π}{6}$,AB=2AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a<c<b | B. | a<b<c | C. | c<a<b | D. | b<a<c |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1009}{1008}$ | B. | $\frac{2015}{1007}$ | C. | $\frac{2016}{2015}$ | D. | $\frac{2015}{2014}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 26 | B. | 31 | C. | 36 | D. | 37 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{BO}=-\frac{3}{4}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$ | B. | $\overrightarrow{BO}=-\frac{1}{4}\overrightarrow{AB}+\frac{1}{4}\overrightarrow{AC}$ | C. | $\overrightarrow{BO}=\frac{3}{4}\overrightarrow{AB}-\frac{1}{4}\overrightarrow{AC}$ | D. | $\overrightarrow{BO}=-\frac{1}{2}\overrightarrow{AB}-\frac{1}{4}\overrightarrow{AC}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com