
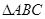 是边长为
是边长为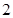 的正三角形,
的正三角形,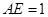 ,
,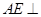 平面
平面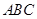 ,平面
,平面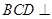 平面
平面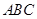 ,
,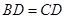 ,且
,且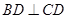 .
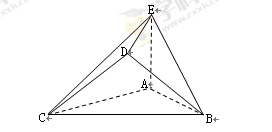
.
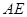 //平面
//平面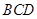 ;
;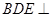 平面
平面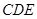 ;
;
 的中点
的中点 ,根据等腰三角形中线即为高线可得
,根据等腰三角形中线即为高线可得 ,又因为面
,又因为面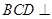 平面
平面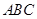 ,根据面面垂直的性质定理可得
,根据面面垂直的性质定理可得 平面
平面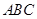 ,已知
,已知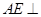 平面
平面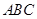 ,所以
,所以 ,根据线面平行的判定定理可得
,根据线面平行的判定定理可得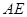 //平面
//平面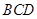 。(2)因为
。(2)因为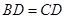 ,且
,且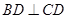 ,斜边中线
,斜边中线 ,又因为
,又因为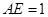 ,
, 可证得
可证得 是平行四边形,可得
是平行四边形,可得 ,根据线面垂直的判定定理可证得
,根据线面垂直的判定定理可证得 平面
平面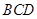 ,即
,即 平面
平面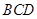 ,从而可得
,从而可得 ,又因为
,又因为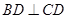 即可证得
即可证得 平面
平面 ,从而证得平面
,从而证得平面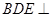 平面
平面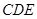 。(3)根据前两问的条件可证得
。(3)根据前两问的条件可证得 平面
平面 ,从而可将此几何体分割为以四边形
,从而可将此几何体分割为以四边形 为底面的两个四棱锥,然后再求其体积。
为底面的两个四棱锥,然后再求其体积。 的中点
的中点 ,连接
,连接 、
、 ,
,
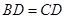 ,可得:
,可得: ,
, 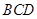 ⊥平面
⊥平面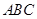 ,平面
,平面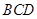
 平面
平面 ,
,  平面
平面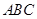 ,
, 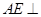 平面
平面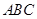 , 所以
, 所以 ,
,  平面
平面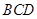 ,
, 平面
平面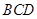 ,
,  平面
平面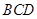 . 4分
. 4分  ,又
,又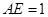 ,
, ,
,  是平行四边形,则有
是平行四边形,则有 ,
,  ,又
,又 ,
,

 平面
平面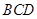 , 所以
, 所以 平面
平面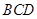 ,
,  平面
平面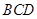 ,所以
,所以 ,
,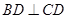 ,
,  ,
,
 平面
平面 ,
,  平面
平面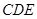 , 所以平面
, 所以平面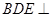 平面
平面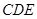 . 10分
. 10分  ,
,
 平面
平面 , 11分
, 11分 ,易得四边形
,易得四边形 为矩形其面积
为矩形其面积 , 12分
, 12分 =
= . 14分
. 14分

 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:高中数学 来源:不详 题型:解答题
 AC
AC B的大小为60°.过P作PH⊥EF于H.
B的大小为60°.过P作PH⊥EF于H.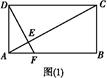
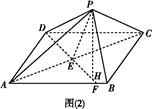
 ABC体积的最大值.
ABC体积的最大值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 A1B1C1中,∠BAC=90°,AB=AC=
A1B1C1中,∠BAC=90°,AB=AC=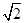 ,AA1=3,D是BC的中点,点E在棱BB1上运动.
,AA1=3,D是BC的中点,点E在棱BB1上运动.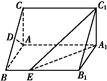
 A1B1E的体积.
A1B1E的体积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com