

 a2h.
a2h. ,BE=
,BE= ,∠DBE=60°,
,∠DBE=60°, BD·BEsin∠DBE=
BD·BEsin∠DBE= a2,S△A1B1C1=
a2,S△A1B1C1= ·A1B1·B1C1sin60°=
·A1B1·B1C1sin60°= a2.
a2. h(S△BDE+S△A1B1C1+
h(S△BDE+S△A1B1C1+ )
) h
h =
= a2h.
a2h.
 a2,S△DBF=
a2,S△DBF= S△ABC=
S△ABC= a2,(4分)
a2,(4分) h(S△DBF+S△A1B1C1+
h(S△DBF+S△A1B1C1+ )
) h(
h( a2+
a2+ a2+
a2+ )=
)= a2h.(8分)
a2h.(8分) a2=
a2= a2h,(10分)
a2h,(10分) a2h-
a2h- a2h=
a2h= a2h.(14分)
a2h.(14分)

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案科目:高中数学 来源:不详 题型:解答题

 OBED的体积.
OBED的体积.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图(2)所示).
的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图(2)所示).
 上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求点G到平面ACD的距离;若不存在,请说明理由.
上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求点G到平面ACD的距离;若不存在,请说明理由.查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题

查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
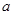 的正方体
的正方体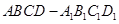 中分离出来的.
中分离出来的.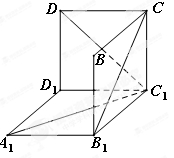
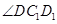 在图中的度数和它表示的角的真实度数都是
在图中的度数和它表示的角的真实度数都是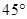 ;
;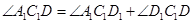 ;
;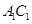 与
与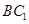 所成的角是
所成的角是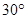 ;
;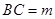 ,则用图示中这样一个装置盛水,最多能盛
,则用图示中这样一个装置盛水,最多能盛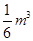 的水.
的水.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com