
 的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图(2)所示).
的中点.沿直径AB折起,使两个半圆所在平面互相垂直(如图(2)所示).
 上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求点G到平面ACD的距离;若不存在,请说明理由.
上是否存在点G,使得FG∥平面ACD?若存在,试指出点G的位置,并求点G到平面ACD的距离;若不存在,请说明理由.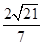
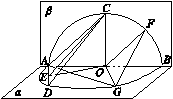
 的中点,∴∠FOB=45°,
的中点,∴∠FOB=45°, 上存在点G,使得FG∥平面ACD,联结OG,如图.
上存在点G,使得FG∥平面ACD,联结OG,如图. 上存在点G,使得FG∥平面ACD,且点G为
上存在点G,使得FG∥平面ACD,且点G为 的中点.
的中点.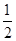 ·AD·CE=
·AD·CE=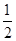 ×2×
×2×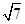 =
=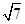 ,S△GAD=S△OAD=
,S△GAD=S△OAD=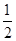 ×2×
×2×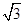 =
=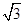 ,
,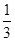 ×
×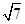 ×h=
×h=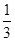 ×
×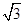 ×2,则h=
×2,则h=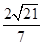 .
.

 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源:不详 题型:解答题
 A1B1C1中,∠BAC=90°,AB=AC=
A1B1C1中,∠BAC=90°,AB=AC=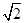 ,AA1=3,D是BC的中点,点E在棱BB1上运动.
,AA1=3,D是BC的中点,点E在棱BB1上运动.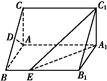
 A1B1E的体积.
A1B1E的体积.查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
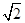 ,AC=2,若四面体ABCD体积的最大值为
,AC=2,若四面体ABCD体积的最大值为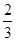 ,则这个球的表面积为( )
,则这个球的表面积为( )A.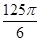 | B.8π | C.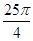 | D.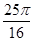 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
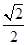 ,
,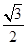 ,
,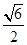 ,则该三棱锥外接球的表面积为( )
,则该三棱锥外接球的表面积为( )| A.2π | B.6π | C.4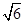 π π | D.24π |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.S1>S2>S3,V1>V2>V3 |
| B.S1<S2<S3,V1<V2<V3 |
| C.S1>S2>S3,V1=V2=V3 |
| D.S1<S2<S3,V1=V2=V3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
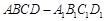 中,点
中,点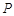 在面对角线
在面对角线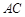 上运动,给出下列四个命题:
上运动,给出下列四个命题: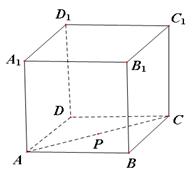
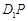 ∥平面
∥平面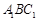 ; ②
; ②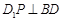 ;
;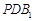 ⊥平面
⊥平面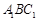 ;④三棱锥
;④三棱锥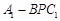 的体
的体查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com