
| X | 4 | 5 | 6 | 7 | 8 | 9 |
| 频数 | 1 | 2 | 26 | 40 | 29 | 2 |
分析 (1)由题意得随机抽取的100个成绩的分布列,由此求出E(X),D(X),由此能求出μ,σ2=.
(2)由(1)知X~N(7,0.8),从而P(7.9<X≤8.8)=$\frac{1}{2}$[P(5.2<X≤8.8)-P(6.1<X≤7.9)]=0.1359.由此能求出这个军区新兵50m步枪射击个人平均成绩在区间(7.9.8.8]上的人数.
解答 解:(1)由题意得随机抽取的100个成绩的分布列为:
| X | 4 | 5 | 6 | 7 | 8 | 9 |
| 频率 | 0.01 | 0.02 | 0.26 | 0.40 | 0.29 | 0.02 |
点评 本题考查总体数学期望、方差的求法,考查概率的求法及应用,是中档题,解题时要认真审题,注意离散型随机变量的分布列的性质的合理运用.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
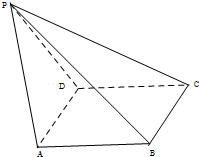 (Ⅰ)证明:PB⊥AD;
(Ⅰ)证明:PB⊥AD;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,已知直线MA切圆O于点A,割线MCB交圆O于点C,B两点,∠BMA的角平分线分别与AC,AB交于E,D两点.
如图,已知直线MA切圆O于点A,割线MCB交圆O于点C,B两点,∠BMA的角平分线分别与AC,AB交于E,D两点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{9}$ | B. | $\frac{9}{16}$ | C. | $\frac{3}{4}$ | D. | $\frac{4}{9}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | m⊆A | B. | m∉A | C. | {m}⊆A | D. | {m}∈A |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1} | B. | {1,2} | C. | {1,2,3} | D. | {1,2,3,4} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com