
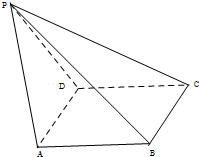
 (Ⅰ)证明:PB⊥AD;
(Ⅰ)证明:PB⊥AD;分析 (Ⅰ)取AD的中点E,连接PE,BD,BE,推导出BE⊥AD,PE⊥AD,从而AD⊥面PBE,由此能证明AD⊥PB.
(Ⅱ)作PO⊥BE于E,PO⊥面ABCD,求出$PO=PB•sin{30°}=\frac{3}{2}$,由此能求出四棱锥P-ABCD的体积.
解答 证明:(Ⅰ)取AD的中点E,连接PE,BD,BE,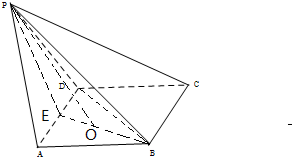
∵底面ABCD为菱形,∠DAB=60°,∴△ABD为正三角形,
又∵E为AD的中点,∴BE⊥AD,
∵侧面PAD为正三角形,E为AD的中点,∴PE⊥AD,
∴AD⊥面PBE,∴AD⊥PB.…(6分)
解:(Ⅱ)由(Ⅰ)AD⊥面PBE,得面ABCD⊥面PBE,
作PO⊥BE于O,PO⊥面ABCD,
∵侧面PAD为边长等于2的正三角形、△ABD为正三角形,E为AD的中点,
∴$PE=BE=\sqrt{3}$,
又∵PB=3,设PB的中点为F,$EF=\sqrt{E{B^2}-B{F^2}}=\frac{{\sqrt{3}}}{2}$,…(8分)
∴$sin∠EBP=\frac{EF}{EB}=\frac{1}{2}$,∴∠EBP=30°,∴$PO=PB•sin{30°}=\frac{3}{2}$,…(10分)
∴四棱锥P-ABCD的体积${V_{P-ABCD}}=\frac{1}{3}×2×\sqrt{3}×\frac{3}{2}=\sqrt{3}$…(12分)
点评 本题考查线线垂直的证明,考查四棱锥的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.


 第三学期赢在暑假系列答案
第三学期赢在暑假系列答案 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | {3,4,5} | B. | {-2,-1,0,1} | ||
| C. | {-5,-4,-3,-2,-1,0,1} | D. | {-5,-4,-3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p是q的必要不充分条件 | B. | ¬q是p的必要不充分条件 | ||
| C. | ¬p是¬q的必要不充分条件 | D. | ¬q是¬p的必要不充分条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\left\{{y|0<y<\frac{1}{2}}\right\}$ | B. | {y|0<y<1} | C. | $\left\{{y|\frac{1}{2}<y<1}\right\}$ | D. | ∅ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| X | 4 | 5 | 6 | 7 | 8 | 9 |
| 频数 | 1 | 2 | 26 | 40 | 29 | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com