
【题目】数列![]() ,定义
,定义![]() 为数列
为数列![]() 的一阶差分数列,其中
的一阶差分数列,其中![]() ,(
,( ![]() ),设
),设![]()
(1)若![]() ,求证:
,求证: ![]() 是等比数列,并求出
是等比数列,并求出![]() 的通项公式;
的通项公式;
(2)若![]() ,又数列
,又数列![]() 满足:
满足: ![]() :
:
①求数列![]() 的前
的前![]() 和
和![]() ;
;
②求证:数列![]() 中的任意一项总可以表示成该数列中其他两项之积.
中的任意一项总可以表示成该数列中其他两项之积.
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案科目:高中数学 来源: 题型:
【题目】某商品在近30天内每件的销售价格P(元)与时间t(天)的函数是:P=![]()
该商品的日销售量Q(件)与时间t(天)的函数关系是:Q=﹣t+40(0<t≤30,t∈N*),求这种商品的日销售金额的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2015 年 12 月,华中地区数城市空气污染指数“爆表”,此轮污染为 2015 年以来最严重的污染过程,为了探究车流量与![]() 的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与
的浓度是否相关,现采集到华中某城市 2015 年 12 月份某星期星期一到星期日某一时间段车流量与![]() 的数据如表:
的数据如表:
时间 | 星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 |
车流量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 28 | 30 | 35 | 41 | 49 | 56 | 62 |
(1)由散点图知![]() 与
与![]() 具有线性相关关系,求
具有线性相关关系,求![]() 关于
关于![]() 的线性回归方程;(提示数据:
的线性回归方程;(提示数据: ![]() )
)
(2)利用(1)所求的回归方程,预测该市车流量为 12 万辆时![]() 的浓度.
的浓度.
参考公式:回归直线的方程是![]() ,
,
其中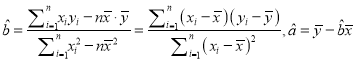 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=﹣x2+ax(a∈R).
(1)当a=3时,求函数f(x)在[![]() ,2]上的最大值和最小值;
,2]上的最大值和最小值;
(2)当函数f(x)在(![]() ,2)单调时,求a的取值范围.
,2)单调时,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】小型风力发电项目投资较少,开发前景广阔.受风力自然资源影响,项目投资存在一定风险.根据测算,IEC(国际电工委员会)风能风区的分类标准如下:
风能分类 | 一类风区 | 二类风区 |
平均风速m/s | 8.5---10 | 6.5---8.5 |
某公司计划用不超过100万元的资金投资于A、B两个小型风能发电项目.调研结果是:未来一年内,位于一类风区的A项目获利![]() %的可能性为0.6,亏损
%的可能性为0.6,亏损![]() %的可能性为0.4;
%的可能性为0.4;
B项目位于二类风区,获利35%的可能性为0.6,亏损10%的可能性是0.2,不赔不赚的可能性是0.2.
假设投资A项目的资金为![]() (
(![]() )万元,投资B项目资金为
)万元,投资B项目资金为![]() (
(![]() )万元,且公司要求对A项目的投资不得低于B项目.
)万元,且公司要求对A项目的投资不得低于B项目.
(Ⅰ)记投资A,B项目的利润分别为![]() 和
和![]() ,试写出随机变量
,试写出随机变量![]() 与
与![]() 的分布列和期望
的分布列和期望![]() ,
, ![]() ;
;
(Ⅱ)根据以上的条件和市场调研,试估计一年后两个项目的平均利润之和![]() 的最大值,并据此给出公司分配投资金额建议.
的最大值,并据此给出公司分配投资金额建议.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知半径为2,圆心在直线y=x+2上的圆C.
(1)当圆C经过点A(2,2)且与y轴相切时,求圆C的方程;
(2)已知E(1,1),F(1,3),若圆C上存在点Q,使|QF|2﹣|QE|2=32,求圆心横坐标a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com