
| P��K2��k�� | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
���� ��1���������⣬n=124��a+b=70��c+d=54��a=43��b=27��c=21��d=33����д��������
��2�����������������������ݼ���۲�ֵ�������ٽ�ֵ�ó����ۣ�
��� �⣺��1�������������ݣ���д2��2���������£�
| ������ | �˶� | �ܼ� | |
| �� | 43 | 27 | 70 |
| ���� | 21 | 33 | 54 |
| �ܼ� | 64 | 60 | 124 |
���� ���⿼���˶����Լ����Ӧ�����⣬�ǻ����⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{��}{12}$ | B�� | $\frac{��}{4}$ | C�� | $\frac{��}{3}$ | D�� | $\frac{��}{6}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | Sn=2Tn | B�� | Tn=2bn+1 | C�� | Tn��an | D�� | Tn��bn+1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
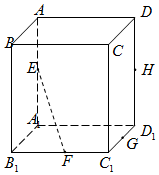 ��ͼ����������ABCD-A1B1C1D1�У�E��F��G��H�ֱ�Ϊ��AA1��B1C1��C1D1��DD1���е㣬������ֱ������ֱ��EF�ཻ���ǣ�������
��ͼ����������ABCD-A1B1C1D1�У�E��F��G��H�ֱ�Ϊ��AA1��B1C1��C1D1��DD1���е㣬������ֱ������ֱ��EF�ཻ���ǣ�������| A�� | ֱ��CC1 | B�� | ֱ��C1D1 | C�� | ֱ��HC1 | D�� | ֱ��GH |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com