
分析 (1)求出f(x)的导数,结合二次函数的性质求出a的范围即可;
(2)依题意得f′(x)=0有两个不同的根x1,x2且x1<x2,即x2-x+a=0有两个不同的根x1,x2且x1<x2,
可得x1+x2=1,x1•x2=a,由(1)得a∈(0,$\frac{1}{4}$).f(x1)+f(x2)=)=$\frac{1}{2}$x12-x1+alnx1=$\frac{1}{2}$x22-x2+alnx2=$\frac{1}{2}[({x}_{1}+{x}_{2})^{2}-2{x}_{2}{x}_{1}]-({x}_{1}+{x}_{2})+a($lnx1+lnx2)=alnaa-a-$\frac{1}{2}$,令g(a)=alna-a-$\frac{1}{2}$,a∈(0,$\frac{1}{4}$).利用导数求解.
解答 解:(1)∵函数f(x)=$\frac{1}{2}$x2-x+alnx的定义域为(0,+∞),
f′(x)=x-1+$\frac{a}{x}$=$\frac{{x}^{2}-x+a}{x}$,
当△=1-4a≤0,即a≥$\frac{1}{4}$时,f′(x)≥0恒成立,此时函数f(x)单调递增,无极值;
当当△=1-4a>0,即a<$\frac{1}{4}$时,∴f′(x)=0有两个不同的根x1,x2且x1<x2,此时函数有两个极值.
综上,a的取值范围(0,$\frac{1}{4}$).
(2)证明:∵f(x)有两个极值点x1,x2且x1<x2,∴f′(x)=0有两个不同的根x1,x2且x1<x2,
∴x2-x+a=0有两个不同的根x1,x2且x1<x2,
∴x1+x2=1,x1•x2=a,由(1)得a∈(0,$\frac{1}{4}$).
f(x1)+f(x2)=)=$\frac{1}{2}$x12-x1+alnx1=$\frac{1}{2}$x22-x2+alnx2
=$\frac{1}{2}[({x}_{1}+{x}_{2})^{2}-2{x}_{2}{x}_{1}]-({x}_{1}+{x}_{2})+a($lnx1+lnx2)=alnaa-a-$\frac{1}{2}$,
令g(a)=alna-a-$\frac{1}{2}$,a∈(0,$\frac{1}{4}$).g′(a)=lna,在a∈(0,$\frac{1}{4}$)时.g′(a)<0恒成立.
∴g(a)在(0,$\frac{1}{4}$)单调递减,故g(a)$>g(\frac{1}{4})$=$\frac{-3-2ln2}{4}$.
∴f(x1)+f(x2)>$\frac{-3-2ln2}{4}$.
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及函数恒成立问题,考查不等式的证明,分类讨论思想,属于中档题.


科目:高中数学 来源: 题型:选择题
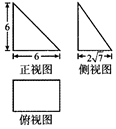 《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的表面积为( )
《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的表面积为( )| A. | 100π cm2 | B. | $\frac{500π}{3}$ cm2 | C. | 400π cm2 | D. | $\frac{4000π}{3}$ cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com