
分析 (Ⅰ)根据题意,分别令n=2,3求出a2,a3,并猜想即${a}_{n}={2}^{n}$,并用数学归纳法证明,即可证明数列{an+1-2an}为常数列,
(Ⅱ)利用放缩法可得$\frac{1}{10}$≤c1+c2+…+cn<$\frac{7}{20}$,即可求出a的范围
解答 解:(Ⅰ)∵数列{an}满足:a1=2,当n∈N*,n>1时,a2+a3+…+an=4(an-1-1),
∴a2=4(a1-1)=4(2-1)=4,
a2+a3=4(a2-1),即4+a3=4(4-1)=12,解得a3=8.
由此猜想{an}是首项为2,公比为2的等比数列,即${a}_{n}={2}^{n}$,
用数学归纳法证明:
①当n=1时,a1=2,成立.
②假设当n=k时,等式成立,即a2+a3+…+ak=4(ak-1-1),
∴22+23+…+2k=4(2k-1-1),
当n=k+1时,a2+a3+…+ak+ak+1
=4(2k-1-1)+2k+1
=2k+1-4+2k+1
=4(2k-1)=4(ak-1),成立,
由①②,得${a}_{n}={2}^{n}$,
∴an+1-2an=2n+1-2•2n=0,
∴数列{an+1-2an}为常数列.
(Ⅱ)∵cn=$\frac{1}{2({a}_{n}+\frac{1}{{a}_{n}})+5}$=$\frac{1}{2({2}^{n}+\frac{1}{{2}^{n}})+5}$,
当n=1时,c1=$\frac{1}{10}$,cn=$\frac{1}{2({2}^{n}+\frac{1}{{2}^{n}})+5}$≤$\frac{1}{{2}^{n+1}}$,
∴c1+c2+…+cn<$\frac{1}{10}$+$\frac{1}{8}$+$\frac{1}{16}$+…+$\frac{1}{{2}^{n+1}}$=$\frac{1}{10}$+$\frac{\frac{1}{8}(1-\frac{1}{{2}^{n-1}})}{1-\frac{1}{2}}$=$\frac{1}{10}$+$\frac{1}{4}$(1-$\frac{1}{{2}^{n-1}}$)<$\frac{1}{10}$+$\frac{1}{4}$=$\frac{7}{20}$,
∴$\frac{1}{10}$=c1<c1+c2+…+cn<$\frac{7}{20}$,
∵对任意n∈N*,2a<c1+c2+…+cn<10a恒成立,
∴$\left\{\begin{array}{l}{2a<\frac{1}{10}}\\{10a≥\frac{7}{20}}\end{array}\right.$,
解得$\frac{7}{200}$≤a<$\frac{1}{20}$,
故实数a的取值范围为[$\frac{7}{200}$,$\frac{1}{20}$).
点评 本题考查了数列的通项公式和数学归纳法和放缩法证明不等式成立,考查了学生的运算能力和转化能力,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| x | 4 | 5 | 6 | 7 | 8 |
| y | 12 | 10 | 9 | 8 | 6 |
| A. | -0.6 | B. | 0.6 | C. | -17.4 | D. | 17.4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2个 | B. | 4个 | C. | 8个 | D. | 无数个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨q | B. | (¬p)∧(¬q) | C. | p∨(¬q) | D. | p∧q |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | Sn=2Tn | B. | Tn=2bn+1 | C. | Tn>an | D. | Tn<bn+1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 6 | 8 | 10 |
| y | 40 | 50 | 70 | 90 | 100 |
| p(K2≥k) | … | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | … |
| k | … | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | … |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
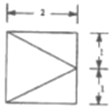 己知四梭锥.它的底面是边长为2的正方形.其俯视图如图所示,左视图为直角三角形,则四棱锥的外接球的表面枳为( )
己知四梭锥.它的底面是边长为2的正方形.其俯视图如图所示,左视图为直角三角形,则四棱锥的外接球的表面枳为( )| A. | 8π | B. | 12π | C. | 4π | D. | 16π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com