
| x | 2 | 4 | 6 | 8 | 10 |
| y | 40 | 50 | 70 | 90 | 100 |
| p(K2≥k) | … | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | … |
| k | … | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | … |
分析 (1)首先做出x,y的平均数,代入b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$,a=$\overline{y}$-b$\overline{x}$,求出线性回归直线的方程的系数,写出回归直线的方程,
(2)将x=12代入回归方程得出y,即销售收入y的估计值.
解答 解:(1)由题意知$\overline{x}=\frac{2+4+6+8+10}{5}=6$,$\overline{y}=\frac{40+50+70+90+100}{5}=70$
$\widehat{b}=\frac{(80+200+420+720+1000)-5×6×70}{(4+16+36+64+100)-5×36}$=8
a=$\overline{y}$-b$\overline{x}$=70-8×6=22,
所以回归直线方程为:$\stackrel{∧}{y}$=8x+22;
(2)当x=12时y=118,因此估计得到当广告费用为12万元时销售收入为118万元.
点评 本题考查回归直线方程的应用,回归直线方程的求法,考查计算能力,属于中档题.


 备战中考寒假系列答案
备战中考寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,+∞) | C. | (0,+∞) | D. | (0,1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
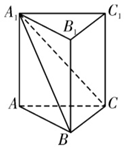 在我国古代数学名著《九章算术》中将底面为直角三角形,且侧棱垂直于底面的三棱柱称之为堑堵,如图,在堑堵ABC-A1B1C1中,AB=BC,AA1>AB,堑堵的顶点C1到直线A1C的距离为m,C1到平面A1BC的距离为n,则$\frac{m}{n}$的取值范围是( )
在我国古代数学名著《九章算术》中将底面为直角三角形,且侧棱垂直于底面的三棱柱称之为堑堵,如图,在堑堵ABC-A1B1C1中,AB=BC,AA1>AB,堑堵的顶点C1到直线A1C的距离为m,C1到平面A1BC的距离为n,则$\frac{m}{n}$的取值范围是( )| A. | (1,$\frac{2\sqrt{3}}{3}$) | B. | ($\frac{\sqrt{2}}{2}$,$\frac{2\sqrt{3}}{3}$) | C. | ($\frac{2\sqrt{3}}{3}$,$\sqrt{3}$) | D. | ($\frac{2\sqrt{3}}{3}$,$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| 男 | 女 | 总计 | |
| 喜欢 | 40 | 20 | 60 |
| 不喜欢 | 20 | 30 | 50 |
| 总计 | 60 | 50 | 110 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
| A. | 在犯错误的概率不超过0.1%的前提下,认为“喜欢该节目与性别有关” | |
| B. | 在犯错误的概率不超过0.1%的前提下,认为“喜欢该节目与性别无关” | |
| C. | 有99%以上的把握认为“喜欢该节目与性别有关” | |
| D. | 有99%以上的把握认为“喜欢该节目与性别无关” |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com