练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    4．在1907年的一项关于16艘轮船的研究中，船的吨位区间从192t～3246t，船员的人数从5人到32人，由船员人数关于吨位的回归分析得到如下结果：$\widehat{y}$=9.5+0.0062x，假定的两艘轮船的吨位相差1000t，船员平均人数相差6人，对于最小的船估计的船员人数是11人，对于最大的船估计的船员人数是31人．

    分析 根据回归方程，计算两艘轮船吨位相差1000吨时船员平均人数的差值，
    以及x=192和x=3246t时，对应$\widehat{y}$的值即可．

    解答 解：由题意，由于船员人数关于吨位的回归方程是：
    $\widehat{y}$=9.5+0.0062x，
    两艘轮船吨位相差1000吨时，
    船员平均人数的差值是0.0062×1000≈6（人）；
    当x=192t时，由回归方程计算$\widehat{y}$=9.5+0.0062×192≈11（人）；
    当x=3246t时，由回归方程计算$\widehat{y}$=9.5+0.0062×3246≈31（人）；
    所以，两艘轮船的吨位相差1000t，船员平均人数相差6人，
    对于最小的船估计的船员人数是11人，对于最大的船估计的船员人数是31人．
    故答案为：6，11，31．

    点评 本题考查了线性回归方程的应用问题，是基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

    6．设函数f（x）=ex+sinx（e为自然对数的底数），g（x）=ax，F（x）=f（x）-g（x）．
    （1）若a=2，且直线x=t（t≥0）分别与函数f（x）和g（x）的图象交于P，Q，求P，Q两点间的最短距离；
    （2）若x≥0时，函数y=F（x）的图象恒在y=F（-x）的图象上方，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知α∈[0，π），在直角坐标系xOy中，直线l1的参数方程为$\left\{\begin{array}{l}{x=tcosα}\\{y=tsinα}\end{array}\right.$（t为参数）；在以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，直线l2的极坐标方程是ρcos（θ-α）=2sin（α+$\frac{π}{6}$）．
    （Ⅰ）求证：l1⊥l2
    （Ⅱ）设点A的极坐标为（2，$\frac{π}{3}$），P为直线l1，l2的交点，求|OP|•|AP|的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

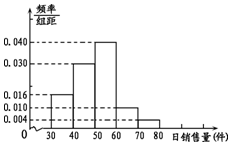    4．某超市计划销售某种产品，先试销该产品n天，对这n天日销售量进行统计，得到频率分布直方图如图．
    （Ⅰ）若已知销售量低于50的天数为23，求n；
    （Ⅱ）厂家对该超市销售这种产品的日返利方案为：每天固定返利45元，另外每销售一件产品，返利3元；频率估计为概率．依此方案，估计日返利额的平均值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知点P在椭圆C1：$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{4}$=1上，点Q在椭圆C2：$\frac{{y}^{2}}{9}$+x2=1上，O为坐标原点，记ω=$\overrightarrow{OP}$•$\overrightarrow{OQ}$，集合{（P，Q）|ω=$\overrightarrow{OP}$•$\overrightarrow{OQ}$}，当ω取得最大值时，集合中符合条件的元素有几个（　　）
    A．2个B．4个C．8个D．无数个

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．求棱长为a的正四面体的内切球和外接球的体积之比．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知命题p：?x＜1，$log{\;}_{\frac{1}{3}}x＜0$；命题q：?x0∈R，$x_0^2≥{2^{x_0}}$，则下列命题中为真命题的是（　　）
    A．p∨qB．（￢p）∧（￢q）C．p∨（￢q）D．p∧q

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    13．某种产品的广告费用支出x（万元）与销售额y（万元）之间有如下的对应数据：
    x246810
    y40507090100
    （1）请根据上表提供的数据，用最小二乘法求出y关于x 的线性回归方程$\stackrel{∧}{y}$=bx+a

    p（K2≥k）…0.100.050.0250.0100.0050.001…
    k…2.7063.8415.0246.6357.87910.828…
    （其中：b=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$，a=$\overline{y}$-b$\overline{x}$　）求回归直线方程．
    （2）据此估计广告费用为12时，销售收入y的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    14．已知函数f（x）=lnx-mx2+（1-2m）x+1
    （I）当m=1时，求曲线f（x）在点（1，f（1））处的切线方程；
    （II）若m∈Z，关于x的不等式f（x）≤0恒成立，求m的最小值．

    查看答案和解析>>

    同步练习册答案