
分析 (Ⅰ)直线l1的参数方程为$\left\{\begin{array}{l}{x=tcosα}\\{y=tsinα}\end{array}\right.$(t为参数);消去参数t可得:直线l1的普通方程.又直线l2的极坐标方程是ρcos(θ-α)=2sin(α+$\frac{π}{6}$).展开为ρcosθcosα+ρsinθsinα=2sin(α+$\frac{π}{6}$).利用互化公式可得直线l2的直角坐标方程,根据两直线垂直的条件即可证明:l1⊥l2.
(Ⅱ)当ρ=2,$θ=\frac{π}{3}$时,满足方程ρcos(θ-α)=2sin(α+$\frac{π}{6}$).可得点A(2,$\frac{π}{3}$),在直线ρcos(θ-α)=2sin(α+$\frac{π}{6}$)上.设点P到直线OA的距离为d,由l1⊥l2可知,d的最大值为$\frac{|OA|}{2}$=1.即可得出|OP|•|AP|=d•|OA|=2d最大值.
解答 解:(Ⅰ)证明:直线l1的参数方程为$\left\{\begin{array}{l}{x=tcosα}\\{y=tsinα}\end{array}\right.$(t为参数);
消去参数t可得:直线l1的普通方程为:xsinα-ycosα=0.
又直线l2的极坐标方程是ρcos(θ-α)=2sin(α+$\frac{π}{6}$).展开为ρcosθcosα+ρsinθsinα=2sin(α+$\frac{π}{6}$).
即直线l2的直角坐标方程为:xcosα+ysinα-2sin(α+$\frac{π}{6}$)=0.
因为sinαcosα+(-cosα)sinα=0,
根据两直线垂直的条件可知,l1⊥l2.
(Ⅱ)当ρ=2,$θ=\frac{π}{3}$时,ρcos(θ-α)=2cos$(\frac{π}{3}-α)$=2sin(α+$\frac{π}{6}$).
所以点A(2,$\frac{π}{3}$),在直线ρcos(θ-α)=2sin(α+$\frac{π}{6}$)上.
设点P到直线OA的距离为d,由l1⊥l2可知,d的最大值为$\frac{|OA|}{2}$=1.
于是|OP|•|AP|=d•|OA|=2d≤2
所以|OP|•|AP|的最大值为2.
点评 本题考查了参数方程化为普通方程、直角坐标方程与极坐标方程的互化、互相垂直的直线斜率之间的关系,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,cos∠ABC=$\frac{1}{3}$,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{{4\sqrt{3}}}{3}$,则△ABC的面积为2$\sqrt{2}$.
如图,在△ABC中,cos∠ABC=$\frac{1}{3}$,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{{4\sqrt{3}}}{3}$,则△ABC的面积为2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 |
| y | 25 | 30 | 40 | 45 |
| A. | 59.5 | B. | 52.5 | C. | 56 | D. | 63.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,+∞) | C. | (0,+∞) | D. | (0,1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
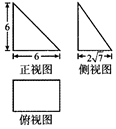 《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的表面积为( )
《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(单位:cm),则该阳马的外接球的表面积为( )| A. | 100π cm2 | B. | $\frac{500π}{3}$ cm2 | C. | 400π cm2 | D. | $\frac{4000π}{3}$ cm2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {4} | B. | {5} | C. | [4,5] | D. | {4,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com