练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．已知集合A={x∈R|0＜x≤5}，B={x∈R|log2x＜2}，则（∁AB）∩Z=（　　）
    A．{4}B．{5}C．[4，5]D．{4，5}

    分析 先求出集合A和B，从而求出CAB，由此能求出（∁AB）∩Z的值．

    解答 解：∵集合A={x∈R|0＜x≤5}，
    B={x∈R|log2x＜2}={x|0＜x＜4}，
    ∴CAB={x|4≤x≤5}，
    ∴（∁AB）∩Z=[4，5]．
    故选：C．

    点评 本题考查交集、补集的求法，是基础题，解题时要认真审题，注意交集、补集定义的合理运用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    9．已知单位向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=0，0≤x≤$\frac{1}{2}$≤y≤1，则|x$\overrightarrow{a}$+y$\overrightarrow{b}$+（1-x-y）$\overrightarrow{c}$|的最小值为$\frac{1}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知两组数据x，y的对应值如下表，若已知x，y是线性相关的且线性回归方程为：$\hat y=\hat bx+\hat a$，经计算知：$\hat b=-1.4$，则$\hat a$=（　　）
    x45678
    y1210986
    A．-0.6B．0.6C．-17.4D．17.4

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．已知α∈[0，π），在直角坐标系xOy中，直线l1的参数方程为$\left\{\begin{array}{l}{x=tcosα}\\{y=tsinα}\end{array}\right.$（t为参数）；在以坐标原点O为极点，x轴的正半轴为极轴的极坐标系中，直线l2的极坐标方程是ρcos（θ-α）=2sin（α+$\frac{π}{6}$）．
    （Ⅰ）求证：l1⊥l2
    （Ⅱ）设点A的极坐标为（2，$\frac{π}{3}$），P为直线l1，l2的交点，求|OP|•|AP|的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    14．在区间（0，5）内任取一个实数m，则满足3＜m＜4的概率为$\frac{1}{5}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

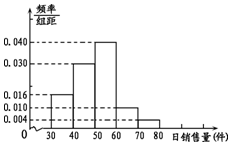    4．某超市计划销售某种产品，先试销该产品n天，对这n天日销售量进行统计，得到频率分布直方图如图．
    （Ⅰ）若已知销售量低于50的天数为23，求n；
    （Ⅱ）厂家对该超市销售这种产品的日返利方案为：每天固定返利45元，另外每销售一件产品，返利3元；频率估计为概率．依此方案，估计日返利额的平均值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．已知点P在椭圆C1：$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{4}$=1上，点Q在椭圆C2：$\frac{{y}^{2}}{9}$+x2=1上，O为坐标原点，记ω=$\overrightarrow{OP}$•$\overrightarrow{OQ}$，集合{（P，Q）|ω=$\overrightarrow{OP}$•$\overrightarrow{OQ}$}，当ω取得最大值时，集合中符合条件的元素有几个（　　）
    A．2个B．4个C．8个D．无数个

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    16．已知命题p：?x＜1，$log{\;}_{\frac{1}{3}}x＜0$；命题q：?x0∈R，$x_0^2≥{2^{x_0}}$，则下列命题中为真命题的是（　　）
    A．p∨qB．（￢p）∧（￢q）C．p∨（￢q）D．p∧q

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

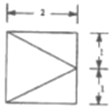    17．己知四梭锥．它的底面是边长为2的正方形．其俯视图如图所示，左视图为直角三角形，则四棱锥的外接球的表面枳为（　　）
    A．8πB．12πC．4πD．16π

    查看答案和解析>>

    同步练习册答案