已知单位向量$\overrightarrow{a}$.$\overrightarrow{b}$.$\overrightarrow{c}$满足$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=0.0≤x≤$\frac{1}{2}$≤y≤1.则|x$\overrightarrow{a}$+y$\overrightarrow 题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

9．已知单位向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=0，0≤x≤$\frac{1}{2}$≤y≤1，则|x$\overrightarrow{a}$+y$\overrightarrow{b}$+（1-x-y）$\overrightarrow{c}$|的最小值为$\frac{1}{4}$．

分析单位向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=0，不妨设$\overrightarrow{a}$=（-1，0），$\overrightarrow{b}$=（$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$），$\overrightarrow{c}$=（$\frac{1}{2}$，-$\frac{\sqrt{3}}{2}$），x$\overrightarrow{a}$+y$\overrightarrow{b}$+（1-x-y）$\overrightarrow{c}$=x（$\overrightarrow{a}-\overrightarrow{c}$）+y$（\overrightarrow{b}-\overrightarrow{c}$）+$\overrightarrow{c}$=（-$\frac{3}{2}x+\frac{1}{2}$，$\frac{\sqrt{3}}{2}x+\sqrt{3}y-\frac{\sqrt{3}}{2}$），
则|x$\overrightarrow{a}$+y$\overrightarrow{b}$+（1-x-y）$\overrightarrow{c}$|²=（-$\frac{3}{2}$x+$\frac{1}{2}$）²+（$\frac{\sqrt{3}}{2}x+\sqrt{3}y-\frac{\sqrt{3}}{2}$）²，再利用柯西不等式求解．

解答解：单位向量$\overrightarrow{a}$，$\overrightarrow{b}$，$\overrightarrow{c}$满足$\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$=0，不妨设$\overrightarrow{a}$=（-1，0），$\overrightarrow{b}$=（$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$），$\overrightarrow{c}$=（$\frac{1}{2}$，-$\frac{\sqrt{3}}{2}$）（如图），
x$\overrightarrow{a}$+y$\overrightarrow{b}$+（1-x-y）$\overrightarrow{c}$=x（$\overrightarrow{a}-\overrightarrow{c}$）+y$（\overrightarrow{b}-\overrightarrow{c}$）+$\overrightarrow{c}$=（-$\frac{3}{2}x+\frac{1}{2}$，$\frac{\sqrt{3}}{2}x+\sqrt{3}y-\frac{\sqrt{3}}{2}$），
∴|x$\overrightarrow{a}$+y$\overrightarrow{b}$+（1-x-y）$\overrightarrow{c}$|²=（-$\frac{3}{2}$x+$\frac{1}{2}$）²+（$\frac{\sqrt{3}}{2}x+\sqrt{3}y-\frac{\sqrt{3}}{2}$）²，
由柯西不等式得=[（-$\frac{3}{2}$x+$\frac{1}{2}$）²+（$\frac{\sqrt{3}}{2}x+\sqrt{3}y-\frac{\sqrt{3}}{2}$）²]•[（$\sqrt{3}$）²+3²]≥[$\sqrt{3}$（-$\frac{3}{2}x+\frac{1}{2}$）+3（$\frac{\sqrt{3}}{2}x+\sqrt{3}y-\frac{\sqrt{3}}{2}$）]²=（3$\sqrt{3}$y-$\sqrt{3}$）²
∵$\frac{1}{2}$≤y≤1，∴y=$\frac{1}{2}$时，（-$\frac{3}{2}$x+$\frac{1}{2}$）²+（$\frac{\sqrt{3}}{2}x+\sqrt{3}y-\frac{\sqrt{3}}{2}$）²最小为$\frac{1}{16}$
则|x$\overrightarrow{a}$+y$\overrightarrow{b}$+（1-x-y）$\overrightarrow{c}$|的最小值为$\frac{1}{4}$．
故答案为：$\frac{1}{4}$．

点评本题考查了向量的模的取值范围的求法，考查了不等式的性质，转化思想，属于中档题．

练习册系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

19．某公司为确定下一年度投入某种产品的宣传费，需要了解年宣传费x（单位：千元）对年销量y（单位：）和利润z（单位：千元）的影响，对近8年的宣传费x_i（i=1，2，…，8）和年销售量y_i数据进行了初步处理，得到下面的散点图及一些统计量的值．

$\overline{x}$	$\overline{y}$	$\overline{w}$	$\sum_{i=1}^{n}$（x_i-$\overline{x}$）²	$\sum_{i=1}^{n}$（w_i-$\overline{w}$）²	$\sum_{i=1}^{n}$（x_i-$\overline{x}$）（y_i-$\overline{y}$）	$\sum_{i=1}^{n}$（w_i-$\overline{w}$）（y_i-$\overline{y}$）
46.6	563	6.8	289.8	1.6	1469	108.8

表中w_i=$\sqrt{{x}_{i}}$，$\overline{w}$=$\frac{1}{8}$$\sum_{i=1}^{8}$w_i
（1）根据散点图判断，$y=a+bx，y=c+d\sqrt{x}$哪一个更适合作为年销售量y关于年宣传费x的回归方程类型（给出判断即可，不必说明理由）；
（2）根据（1）的判断结果及表中数据，建立y关于x的回归方程；
（3）已知这种产品的年利润z与x，y的关系为z=0.2y-x，根据（2）的结果回答下列问题；
①当年宣传费x=90时，年销售量及年利润的预报值是多少？
②当年宣传费x为何值时，年利润的预报值最大？
附：对于一组数据（u₁，v₁），（u₂，v₂），…，（u_n，v_n），其回归线v=α+βu的斜率和截距的最小二乘估计分别为：
$\widehat{β}$=$\frac{\sum_{i=1}^{n}（{μ}_{i}-\overline{μ}）（{v}_{i}-\overline{v}）}{\sum_{i=1}^{n}（{μ}_{i}-\overline{μ}）^{2}}$，$\widehat{a}$=$\overline{v}$-$\widehat{β}$$\overline{μ}$．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

20．锐角△ABC中，D为BC的中点，满足∠BAD+∠C=90°，则角B，C的大小关系为B=C．（填“B＜C”或“B=C”或B＞C）

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

17．

如图，在△ABC中，cos∠ABC=$\frac{1}{3}$，AB=2，点D在线段AC上，且AD=2DC，BD=$\frac{{4\sqrt{3}}}{3}$，则△ABC的面积为2$\sqrt{2}$．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

4．在平面直角坐标系xOy中，将函数y=sin2x的图象向左平移$\frac{π}{12}$个单位得到函数g（x）的图象，则g（$\frac{π}{12}$）的值为$\frac{\sqrt{3}}{2}$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

14．现从某班的一次期末考试中，随机的抽取了七位同学的数学（满分150分）、物理（满分110分）成绩如表所示，数学、物理成绩分别用特征量t，y表示，

特征量	1	2	3	4	5	6	7
t	101	124	119	106	122	118	115
y	74	83	87	75	85	87	83

（1）求y关于t的回归方程；
（2）利用（1）中的回归方程，分析数学成绩的变化对物理成绩的影响，并估计该班某学生数学成绩130分时，他的物理成绩（精确到个位）．
附：回归方程$\widehaty=\widehatbt+\widehata$中斜率和截距的最小二乘估计公式分别为：$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{t}_{i}-\overline{t}）^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$-$\stackrel{∧}{b}$$\overline{t}$．${\sum_{i=1}^7{（{{t_i}-\overline t}）}^2}=432$．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

1．

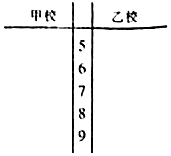某市对创“市级示范性学校”的甲、乙两所学校进行复查验收，对办学的社会满意度一项评价随机访问了20位市民，这20位市民对这两所学校的评分（评分越高表明市民的评价越好）的数据如下：
甲校：58，66，71，58，67，72，82，92，83，86，67，59，86，72，78，59，68，69，73，81；
乙校：90，80，73，65，67，69，81，85，82，88，89，86，86，78，98，95，96，91，76，69，．
检查组将成绩分成了四个等级：成绩在区间[85，100]的为A等，在区间[70，85）的为B等，在区间[60，70）的为C等，在区间[0，60）为D等．
（1）请用茎叶图表示上面的数据，并通过观察茎叶图，对两所学校办学的社会满意度进行比较，写出两个统计结论；
（2）根据所给数据，以事件发生的频率作为相应事件发生的概率，求乙校得分的等级高于甲校得分的等级的概率．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

18．已知某产品的广告费用x（单位：万元）与销售额y（单位：万元）具有线性关系关系，其统计数据如下表：

x	3	4	5	6
y	25	30	40	45

由上表可得线性回归方程$\widehat{y}$=$\widehat{b}$x+$\widehat{a}$，据此模型预报广告费用为8万元时的销售额是（　　）
附：$\widehat{b}$=$\frac{{\sum_{i=1}^n{（{x_i}-\overline x）•（{y_i}-\overline y）}}}{{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}}=\frac{{\sum_{i=1}^n{{x_i}{y_i}-n\overline x\overline y}}}{{\sum_{i=1}^n{x_i^2}-n{{（\overline x）}^2}}}$；$\widehat{a}$=$\widehat{y}$-$\widehat{b}$x．

A．

59.5

B．

52.5

C．

D．

63.5

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

19．已知集合A={x∈R|0＜x≤5}，B={x∈R|log₂x＜2}，则（∁_AB）∩Z=（　　）

A．

{4}

B．

{5}

C．

[4，5]

D．

{4，5}

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学