
分析 (1)根据题意可知f(t)=g(t),令h(x)=ex+sinx-x(x≥0),求出其导函数,进而求得h(x)的最小值即为P、Q两点间的最短距离.
(2)令ϕ(x)=F(x)-F(-x)=ex-e-x+2sinx-2ax,函数y=F(x)的图象恒在y=F(-x)的图象上方,等价于ϕ(x)≥0恒成立,求出其导函数,可求出φ(x)的单调性,进而可求得a的取值范围.
解答 解:(1)因为a=2,所以|PQ|=et+sint-2t.令h(x)=ex+sinx-2x,
即h'(x)=ex+cosx-2,因为h''(x)=ex-sinx,
当x>0时,ex>1,-1≤sinx≤1,所以h''(x)=ex-sinx>0,
所以h'(x)=ex+cosx-2在(0,+∞)上递增,所以h'(x)=ex+cosx-2>h'(0)=0,
∴x∈[0,+∞)时,h(x)的最小值为h(0)=1,所以|PQ|min=1.
(2)令ϕ(x)=F(x)-F(-x)=ex-e-x+2sinx-2ax,
则ϕ'(x)=ex-e-x+2cosx-2a,S(x)=ϕ''(x)=ex-e-x-2sinx,
因为S'(x)=ex+e-x-2cosx≥0当x≥0时恒成立,所以函数S(x)在[0,+∞)上单调递增,
∴S(x)≥S(0)=0当x∈[0,+∞)时恒成立;
故函数ϕ'(x)在[0,+∞)上单调递增,所以ϕ'(x)≥ϕ'(0)=4-2a在x∈[0,+∞)时恒成立.
当a≤2时,ϕ'(x)≥0,ϕ(x)在[0,+∞)单调递增,即ϕ(x)≥ϕ(0)=0.
故a≤2时F(x)≥F(-x)恒成立.
当a>2时,因为ϕ'(x)在[0,+∞)单调递增,
所以总存在x0∈(0,+∞),使ϕ(x)在区间[0,x0)上ϕ'(x)<0,即ϕ(x)在区间[0,x0)上单调递减,而ϕ(0)=0,
所以当x∈[0,x0)时,ϕ(x)<0,这与F(x)-F(-x)≥0对x∈[0,+∞)恒成立矛盾,
所以a>2不符合题意,故符合条件的a的取值范围是(-∞,2].
点评 本题主要考查了利用函数的导数求出函数的单调性以及函数的极值问题,考查了转化思想、分类讨论思想,属于中档题


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,在△ABC中,cos∠ABC=$\frac{1}{3}$,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{{4\sqrt{3}}}{3}$,则△ABC的面积为2$\sqrt{2}$.
如图,在△ABC中,cos∠ABC=$\frac{1}{3}$,AB=2,点D在线段AC上,且AD=2DC,BD=$\frac{{4\sqrt{3}}}{3}$,则△ABC的面积为2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 特征量 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| t | 101 | 124 | 119 | 106 | 122 | 118 | 115 |
| y | 74 | 83 | 87 | 75 | 85 | 87 | 83 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
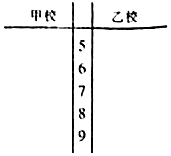 某市对创“市级示范性学校”的甲、乙两所学校进行复查验收,对办学的社会满意度一项评价随机访问了20位市民,这20位市民对这两所学校的评分(评分越高表明市民的评价越好)的数据如下:
某市对创“市级示范性学校”的甲、乙两所学校进行复查验收,对办学的社会满意度一项评价随机访问了20位市民,这20位市民对这两所学校的评分(评分越高表明市民的评价越好)的数据如下:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 物理及格 | 物理不及格 | 合计 | |
| 数学及格 | 28 | 8 | 36 |
| 数学不及格 | 16 | 20 | 36 |
| 合计 | 44 | 28 | 72 |
| P(X2≥k) | 0.150 | 0.100 | 0.050 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 3 | 4 | 5 | 6 |
| y | 25 | 30 | 40 | 45 |
| A. | 59.5 | B. | 52.5 | C. | 56 | D. | 63.5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,+∞) | C. | (0,+∞) | D. | (0,1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com