
分析 根据f(x)的单调性判断m,n的范围,利用对数的运算性质得出mn=1,根据f(x)的单调性得出f(m2)=2,从而可解出m,n的值.
解答 解:f(x)=$\left\{\begin{array}{l}{-lo{g}_{4}x,0<x<1}\\{lo{g}_{4}x,x≥1}\end{array}\right.$,∴f(x)在(0,1)上单调递减,在[1,+∞)上单调递增,
∵f(m)=f(n),
∴m<1<n,且-log4m=log4n,∴mn=1.
∴m2<m<1,
∵f(x)在[m2,n]的最大值为2,
∴f(m2)=2,即-log4m2=2,解得m=$\frac{1}{4}$,
∴n=4,
∴$\frac{n}{m}$=16.
故答案为:16
点评 本题考查了对数函数的性质,属于中档题.


 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:高中数学 来源: 题型:解答题
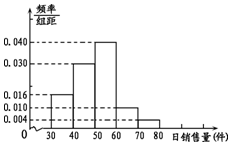 某超市计划销售某种产品,先试销该产品n天,对这n天日销售量进行统计,得到频率分布直方图如图.
某超市计划销售某种产品,先试销该产品n天,对这n天日销售量进行统计,得到频率分布直方图如图.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 6 | 8 | 10 |
| y | 40 | 50 | 70 | 90 | 100 |
| p(K2≥k) | … | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | … |
| k | … | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | … |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
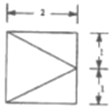 己知四梭锥.它的底面是边长为2的正方形.其俯视图如图所示,左视图为直角三角形,则四棱锥的外接球的表面枳为( )
己知四梭锥.它的底面是边长为2的正方形.其俯视图如图所示,左视图为直角三角形,则四棱锥的外接球的表面枳为( )| A. | 8π | B. | 12π | C. | 4π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 8π | C. | 12π | D. | 16π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
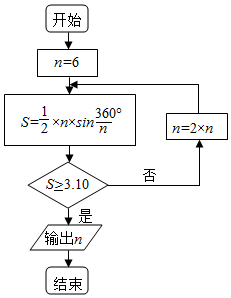 我国魏晋期间的伟大的数学家刘徽,是最早提出用逻辑推理的方式来论证数学命题的人,他创立了“割圆术”,得到了著名的“徽率”,即圆周率精确到小数点后两位的近似值3.14.如图就是利用“割圆术”的思想设计的一个程序框图,则输出的求n的值为(参考数据:sin15°=0.2588,sin7.5°=0.1305)( )
我国魏晋期间的伟大的数学家刘徽,是最早提出用逻辑推理的方式来论证数学命题的人,他创立了“割圆术”,得到了著名的“徽率”,即圆周率精确到小数点后两位的近似值3.14.如图就是利用“割圆术”的思想设计的一个程序框图,则输出的求n的值为(参考数据:sin15°=0.2588,sin7.5°=0.1305)( )| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com