
分析 由题意,设向量$\overrightarrow{a}$,$\overrightarrow{b}$的坐标,利用向量相等得到关于坐标的方程组求出向量$\overrightarrow{a}$,$\overrightarrow{b}$,利用数量积公式求夹角.
解答 解:设向量$\overrightarrow{a}$=(x,y),$\overrightarrow{b}$=(m,n),由已知得到$\overrightarrow{a}$+2$\overrightarrow{b}$=(x+2m,y+2n)=(2,-4),3$\overrightarrow{a}$-$\overrightarrow{b}$=(3x-m,3y-n)=(-8,16),
所以$\left\{\begin{array}{l}{x+2m=2}\\{3x-m=-8}\end{array}\right.$,$\left\{\begin{array}{l}{y+2n=-4}\\{3y-n=16}\end{array}\right.$,分别解之得到$\left\{\begin{array}{l}{x=-2}\\{m=2}\end{array}\right.$,$\left\{\begin{array}{l}{y=4}\\{n=-4}\end{array}\right.$,所以$\overrightarrow{a}$=(-2,4),$\overrightarrow{b}$=(2,-4),
所以向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角的余弦值为$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}=\frac{-20}{\sqrt{20}•\sqrt{20}}$-1,所以向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角的大小为π;
故答案为:π.
点评 本题考查了平面向量的坐标运算;利用方程组的思想是解答本题的关键.


 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案科目:高中数学 来源: 题型:解答题
| x | 2 | 4 | 6 | 8 | 10 |
| y | 40 | 50 | 70 | 90 | 100 |
| p(K2≥k) | … | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 | … |
| k | … | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 | … |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 、$-\frac{1}{2}$ | B. | -1 | C. | $\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{e}f(2)<f(1)$ | B. | $\frac{2}{e}f(2)>f(1)$ | C. | f(1)>0 | D. | f(-1)>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
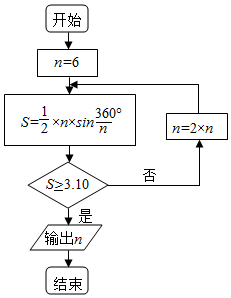 我国魏晋期间的伟大的数学家刘徽,是最早提出用逻辑推理的方式来论证数学命题的人,他创立了“割圆术”,得到了著名的“徽率”,即圆周率精确到小数点后两位的近似值3.14.如图就是利用“割圆术”的思想设计的一个程序框图,则输出的求n的值为(参考数据:sin15°=0.2588,sin7.5°=0.1305)( )
我国魏晋期间的伟大的数学家刘徽,是最早提出用逻辑推理的方式来论证数学命题的人,他创立了“割圆术”,得到了著名的“徽率”,即圆周率精确到小数点后两位的近似值3.14.如图就是利用“割圆术”的思想设计的一个程序框图,则输出的求n的值为(参考数据:sin15°=0.2588,sin7.5°=0.1305)( )| A. | 12 | B. | 24 | C. | 36 | D. | 48 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com