
分析 (Ⅰ)运用等差数列的通项公式和等比数列中项的性质,解方程可得首项和公差,即可得到所求通项公式;
(Ⅱ)化简bn=(-1)n$\frac{n}{(3n-\frac{3}{2})(3n+\frac{3}{2})}$=$\frac{1}{9}$•(-1)n•($\frac{1}{2n-1}$+$\frac{1}{2n+1}$),再由数列的求和方法:裂项相消求和,即可得到所求和.
解答 解:(Ⅰ)在公差d不为0的等差数列{an}中,a22=a3+a6,
且a3为a1与a11的等比中项.
可得(a1+d)2=2a1+7d,且a32=a1a11,即(a1+2d)2=a1(a1+10d),
解得a1=2,d=3,
则an=2+3(n-1)=3n-1,n∈N*;
(Ⅱ)bn=(-1)n$\frac{n}{({a}_{n}-\frac{1}{2})({a}_{n+1}-\frac{1}{2})}$=(-1)n$\frac{n}{(3n-\frac{3}{2})(3n+\frac{3}{2})}$
=$\frac{1}{9}$•(-1)n•$\frac{4n}{(2n-1)(2n+1)}$=$\frac{1}{9}$•(-1)n•($\frac{1}{2n-1}$+$\frac{1}{2n+1}$),
∴Tn=b1+b2+b3+…+bn=$\frac{1}{9}$[-($\frac{1}{1}$+$\frac{1}{3}$)+($\frac{1}{3}$+$\frac{1}{5}$)-($\frac{1}{5}$+$\frac{1}{7}$)+…+(-1)n•($\frac{1}{2n-1}$+$\frac{1}{2n+1}$)]
=$\frac{1}{9}$[-1+(-1)n•$\frac{1}{2n+1}$)].
点评 本题考查等差数列的通项公式的求法,注意运用方程思想,考查数列的求和方法:裂项相消求和,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 物理及格 | 物理不及格 | 合计 | |
| 数学及格 | 28 | 8 | 36 |
| 数学不及格 | 16 | 20 | 36 |
| 合计 | 44 | 28 | 72 |
| P(X2≥k) | 0.150 | 0.100 | 0.050 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{e}f(2)<f(1)$ | B. | $\frac{2}{e}f(2)>f(1)$ | C. | f(1)>0 | D. | f(-1)>0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
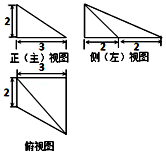
| A. | $2\sqrt{5}$ | B. | $4\sqrt{2}$ | C. | $\sqrt{29}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,3) | B. | $(-\frac{12}{5},-\frac{12}{5})$ | C. | (-3,0) | D. | $(\frac{12}{5},\frac{12}{5})$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com