
���� ������ȥ����t���������C1����ͨ���̣���$\left\{\begin{array}{l}{x=��cos��}\\{y=��sin��}\end{array}\right.$�������������C2��ֱ�����귽�̣�
��������C1��������C2�ķ��̣����A��B�����꣬��������֮��ľ��빫ʽ���������$\frac{|MA|•|MB|}{|AB|}$��ֵ��
��� �⣺����y=$\frac{\sqrt{2}}{2}$t������x=1+$\frac{\sqrt{2}}{2}$t��������x-y-1=0��������C1����ͨ��x-y-1=0��
����${C_2}��\frac{1}{��^2}=\frac{{{{cos}^2}��}}{2}+{sin^2}��$����1=$\frac{{��}^{2}co{s}^{2}��}{2}$+��2sin2�ȣ�
��$\left\{\begin{array}{l}{x=��cos��}\\{y=��sin��}\end{array}\right.$��������C2��ֱ�����귽��$\frac{{x}^{2}}{2}+{y}^{2}=1$��
������$\left\{\begin{array}{l}{y=x-1}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$�������ã�3x2-4x=0����ã�x=0��x=$\frac{4}{3}$��
��A��0��-1����B��$\frac{4}{3}$��$\frac{1}{3}$����
��حMAح=$\sqrt{��1-0��^{2}+��0+1��^{2}}$=$\sqrt{2}$��حMBح=$\sqrt{��\frac{4}{3}-1��^{2}+��\frac{1}{3}-0��^{2}}$=$\frac{\sqrt{2}}{3}$��
��حABح=$\sqrt{��\frac{4}{3}-0��^{2}+��\frac{1}{3}+1��^{2}}$=$\frac{4\sqrt{2}}{3}$��
��$\frac{|MA|•|MB|}{|AB|}$=$\frac{\sqrt{2}��\frac{\sqrt{2}}{3}}{\frac{4\sqrt{2}}{3}}$=$\frac{{\sqrt{2}}}{4}$��
��$\frac{|MA|•|MB|}{|AB|}$��ֵ$\frac{{\sqrt{2}}}{4}$��
���� ���⿼��ֱ�ߵIJ������̣���Բ�ļ����귽�̣�ֱ������Բ��λ�ù�ϵ��������������������е��⣮


 �̲�ȫ���ִʾ�ƪϵ�д�
�̲�ȫ���ִʾ�ƪϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2�� | B�� | 4�� | C�� | 8�� | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
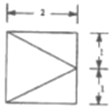 ��֪���������ĵ����DZ߳�Ϊ2�������Σ��丩��ͼ��ͼ��ʾ������ͼΪֱ�������Σ��������������ı�����Ϊ��������
��֪���������ĵ����DZ߳�Ϊ2�������Σ��丩��ͼ��ͼ��ʾ������ͼΪֱ�������Σ��������������ı�����Ϊ��������| A�� | 8�� | B�� | 12�� | C�� | 4�� | D�� | 16�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
| �������� | ���������� | �ϼ� | |
| ��ѧ���� | 28 | 8 | 36 |
| ��ѧ������ | 16 | 20 | 36 |
| �ϼ� | 44 | 28 | 72 |
| P��X2��k�� | 0.150 | 0.100 | 0.050 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 6.635 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com