练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    抛物线y2=16x的焦点坐标是（　　）
    A、（4，0）
    B、（0，4）
    C、（8，0）
    D、（0，8）
    考点：抛物线的简单性质
    专题：计算题,圆锥曲线的定义、性质与方程
    分析：根据抛物线的标准方程，求出p值，确定开口方向，从而写出焦点坐标．
    解答： 解：抛物线y2=16x，开口向右，p=8，
    ∴抛物线y2=16x的焦点坐标是（4，0），
    故选：A．
    点评：本题考查抛物线的标准方程，以及简单性质的应用，属于容易题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    已知函数y=sinax+b（a＞0）某一个周期的图象如图所示，则函数f（x）=ax2+bx+1零点的个数有（　　）
    A、0B、1C、2D、无法确定

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设复数ω=-
    1
    2
    +
    		3
    2
    i（i为虚数单位），则（ω+1）2=（　　）
    A、
    1
    2
    -
    		3
    2
    i
    B、
    1
    2
    +
    		3
    2
    i
    C、-
    1
    2
    -
    		3
    2
    i
    D、-
    1
    2
    +
    		3
    2
    i

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    各大学在高考录取时采取专业志愿优先的录取原则．一考生从某大学所给的7个专业中，选择3个作为自己的第一、二、三专业志愿，其中甲、乙两个专业不能同时兼报，则该考生不同的填报专业志愿的方法有（　　）
    A、210种B、180种
    C、120种D、95种

    查看答案和解析>>

    科目：高中数学 来源： 题型：

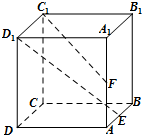    已知点E、F分别是正方体ABCD-A1B1C1D1的棱AB、AA1的中点，点M、N分别是线段D1E与C1F上的点，则满足与平面ABCD平行的直线MN有（　　）
    A、0条B、1条C、2条D、无数条

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f（x）=|x-1|．
    （Ⅰ）解不等式：f（x）+f（x-1）≤2；
    （Ⅱ）当a＞0时，不等式2a-3≥f（ax）-af（x）恒成立，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

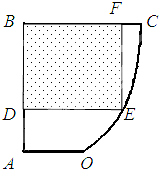    某同学的数学研究性学习课题是：在校内一块不规则土地OABC（测绘图如图所示）规划一个矩形运动场地．经过测量发现AB⊥BC，OA∥BC，曲线段OC可近似看作是以点O为顶点且开口向上的抛物线的一段，OA=20m，AB=BC=40m．
    （1）该同学在测绘图上建立了以O为原点，直线AO为x轴的直角坐标系，请帮他计算曲线段OC对应的函数关系式；
    （2）如果矩形运动场地BDEF的相邻两边分别落在AB，BC上，且一个顶点E落在曲线段OC上，该同学应如何规划才能使运动场地面积最大？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知：各项均为正数的等比数列{an}中，a1=1，a2+2a3=1．
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）将同时满足下列两个条件的数列{cn}称为“约束数列”：①cn＞cn+1（n∈N*）；②存在常数M，使得数列{cn}的前n项和Sn＜M对任意的n∈N*恒成立，试判断数列{an}是否是“约束数列”，并说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    设x，y，z∈R+，x2+y2+z2=1，则S=
    (1+z)2
    2xyz
    的最小值为
     
    ．

    查看答案和解析>>

    同步练习册答案