
分析 (1)根据等比数列和等差数列的通项公式,建立方程组关系求出公比和公差即可得到结论.
(2)根据等比数列和等差数列的前n项和公式进行求解即可.
解答 解:(1)设{an}的公比为q,{bn}的公差为d,由题意q>0,
由已知,有$\left\{{\begin{array}{l}{(1+d)+(1+2d)=2q}\\{{q^2}-3(1+d)=2}\end{array}}\right.$,
即$\left\{{\begin{array}{l}{-2q+3d=-2}\\{{q^2}-3d=5}\end{array}}\right.$,
消去d得:q2-2q-3=0,解得q=3或q=-1(舍去)
∴$d=\frac{4}{3}$,q=3,
所以{an}的通项公式为${a_n}={3^{n-1}}$,n∈N*,
{bn}的通项公式为${b_n}=\frac{4}{3}n-\frac{1}{3}$,n∈N*.
(2)由(1)知an}的通项公式为${a_n}={3^{n-1}}$,n∈N*,则数列为等比数列,则Sn=$\frac{1-{3}^{n}}{1-3}$=$\frac{1}{2}$(3n-1),
{bn}的通项公式为${b_n}=\frac{4}{3}n-\frac{1}{3}$,n∈N*.则数列为等差数列,则Tn=$\frac{(1+\frac{4}{3}n-\frac{1}{3})×n}{2}$=$\frac{2}{3}$n2+$\frac{1}{3}$n,
即${S_n}=\frac{1}{2}({3^n}-1)$,${T_n}=\frac{2}{3}{n^2}+\frac{1}{3}n$.
点评 本题主要考查等比数列和等差数列的通项公式以及前n项和公式的计算,利用方程组法求出等差和等比是解决本题的关键.比较基础.


科目:高中数学 来源: 题型:选择题
| A. | $-\frac{{{e^{2π}}(1-{e^{2016π}})}}{{1-{e^{2π}}}}$ | B. | $-\frac{{{e^{2π}}(1-{e^{1008π}})}}{{1-{e^π}}}$ | ||
| C. | $-\frac{{{e^{2π}}(1-{e^{1008π}})}}{{1-{e^{2π}}}}$ | D. | $-\frac{{{e^{2π}}(1-{e^{2014π}})}}{{1-{e^{2π}}}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
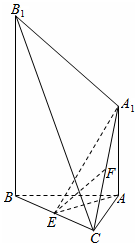 如图,已知AA1⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2$\sqrt{5}$,AA1=$\sqrt{7}$,BB1=2$\sqrt{7}$,点E和F分别为BC和A1C的中点.
如图,已知AA1⊥平面ABC,BB1∥AA1,AB=AC=3,BC=2$\sqrt{5}$,AA1=$\sqrt{7}$,BB1=2$\sqrt{7}$,点E和F分别为BC和A1C的中点. 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com