
【题目】已知![]()
(1)若![]() ,且函数
,且函数![]() 在区间
在区间![]() 上单调递增,求实数a的范围;
上单调递增,求实数a的范围;
(2)若函数![]() 有两个极值点
有两个极值点![]() ,
, ![]() 且存在
且存在![]() 满足
满足![]() ,令函数
,令函数![]() ,试判断
,试判断![]() 零点的个数并证明.
零点的个数并证明.
【答案】(1)![]() (2)函数
(2)函数![]() 有两个零点
有两个零点![]() 和
和![]()
【解析】试题分析:(1)求导后根据函数在区间单调递增,导函数大于或等于0(2)先判断![]() 为一个零点,然后再求导,根据
为一个零点,然后再求导,根据![]() ,化简求得另一个零点。
,化简求得另一个零点。
解析:(1)当![]() 时,
时, ![]() ,因为函数
,因为函数![]() 在
在![]() 上单调递增,
上单调递增,
所以当![]() 时,
时, ![]() 恒成立.
恒成立.
函数![]() 的对称轴为
的对称轴为![]() .
.
①![]() ,即
,即![]() 时,
时, ![]() ,
,
即![]() ,解之得
,解之得![]() ,解集为空集;
,解集为空集;
②![]() ,即
,即![]() 时,
时, ![]()
即![]() ,解之得
,解之得![]() ,所以
,所以![]()
③![]() ,即
,即![]() 时,
时, ![]()
即![]() ,解之得
,解之得![]() ,所以
,所以![]()
综上所述,当![]() 函数
函数![]() 在区间
在区间![]() 上单调递增.
上单调递增.
(2)∵![]() 有两个极值点
有两个极值点![]() ,
,
∴![]() 是方程
是方程![]() 的两个根,且函数
的两个根,且函数![]() 在区间
在区间![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
∵![]()
∴函数![]() 也是在区间
也是在区间![]() 和
和![]() 上单调递增,在
上单调递增,在![]() 上单调递减
上单调递减
∵![]() ,∴
,∴![]() 是函数
是函数![]() 的一个零点.
的一个零点.
由题意知: ![]()
∵![]() ,∴
,∴![]() ,∴
,∴![]() ∴
∴![]() ,∴
,∴![]() 又
又![]()
![]()
∵![]() 是方程
是方程![]() 的两个根,
的两个根,
∴![]() ,
, ![]() ,
,
∴![]()
∵函数![]() 图像连续,且在区间
图像连续,且在区间![]() 上单调递增,在
上单调递增,在![]() 上单调递减,在
上单调递减,在![]() 上单调递增
上单调递增
∴当![]() 时,
时, ![]() ,当
,当![]() 时
时![]() ,当
,当![]() 时
时![]() ,
,
∴函数![]() 有两个零点
有两个零点![]() 和
和![]() .
.


 优加精卷系列答案
优加精卷系列答案科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .
.
(1)求证:数列![]() 为等比数列;
为等比数列;
(2)设数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证: ![]() 为定值;
为定值;
(3)判断数列![]() 中是否存在三项成等差数列,并证明你的结论.
中是否存在三项成等差数列,并证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的首项a1= ![]() ,an+1=
,an+1= ![]() ,n=1,2,…
,n=1,2,…
(1)求证:{ ![]() ﹣1}是等比数列,并求出{an}的通项公式;
﹣1}是等比数列,并求出{an}的通项公式;
(2)证明:对任意的x>0,an≥ ![]() ﹣
﹣ ![]() (
( ![]() ﹣x),n=1,2,…
﹣x),n=1,2,…
(3)证明:n﹣ ![]() ≥a1+a2+…+an>
≥a1+a2+…+an> ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
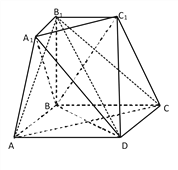
【题目】如图所示的几何体是由棱台![]() 和棱锥
和棱锥![]() 拼接而成的组合体,其底面四边形
拼接而成的组合体,其底面四边形![]() 是边长为
是边长为![]() 的菱形,且
的菱形,且![]() ,
, ![]()
![]() 平面
平面![]() ,
, ![]() .
.
(1)求证:平面![]()
![]() 平面
平面![]()
![]() ;
;
(2)求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市为了解本市2万名学生的汉字书写水平,在全市范围内进行了汉字听写考试,现从某校随机抽取了50名学生,将所得成绩整理后,发现其成绩全部介于![]() 之间,将其成绩按如下分成六组,得到频数分布表
之间,将其成绩按如下分成六组,得到频数分布表
成绩 |
|
|
|
|
|
|
人数 | 4 | 10 | 16 | 10 | 6 | 4 |

(1)在答题卡上作出这些数据的频率分布直方图;
(2)估算该校50名学生成绩的平均值![]() 和中位数(同一组中的数据用该组区间的中点值作代表);
和中位数(同一组中的数据用该组区间的中点值作代表);
(3)以该校50名学生成绩的频率作为概率,试估计该市分数在![]() 的人数.
的人数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com