练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    用数学归纳法证明等式1+3+5+…+（2n﹣1）=n2（n∈N*）的过程中，第二步假设n=k时等式成立，则当n=k+1时应得到（　　）

    　 A． 1+3+5+…+（2k+1）=k2 B． 1+3+5+…+（2k+1）=（k+1）2

    　 C． 1+3+5+…+（2k+1）=（k+2）2 D． 1+3+5+…+（2k+1）=（k+3）2


    B

    考点： 数学归纳法．

    专题： 阅读型．

    分析： 首先由题目假设n=k时等式成立，代入得到等式1+3+5+…+（2k﹣1）=k2．当n=k+1时等式左边=1+3+5++（2k﹣1）+（2k+1）由已知化简即可得到结果．

    解答： 解：因为假设n=k时等式成立，即1+3+5+…+（2k﹣1）=k2

    当n=k+1时，等式左边=1+3+5+…+（2k﹣1）+（2k+1）=k2+（2k+1）=（k+1）2．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    函数y＝sin(x＋θ)·cos(x＋θ)在x＝2时取最大值，则θ的一个值是(　　)

    A．B． C

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设：，：，若是的充分条件，则实数的取值范围

    是        ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    现有6位同学排成一排照相，其中甲、乙二人相邻的排法有　   　种．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知点P（tanα，cosα）在第三象限，则角α的终边在第几象限（　　）

    　 A． 第一象限 B． 第二象限 C． 第三象限 D． 第四象限

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数的反函数是（　　）

    　  A．  B．  

    C．  D．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    有根木料长为6米，要做一个如图的窗框，已知上框架与下框架的高的比为1：2，问怎样利用木料，才能使光线通过的窗框面积最大（中间木档的面积可忽略不计）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某商场的某种商品的年进货量为1万件,分若干次进货,每次进货的量相同,且需运费100元,运来的货物除出售外,还需租仓库存放,一年的租金按一次进货时的一半来计算,每件2元,为使一年的运费和租金最省,每次进货量应为         （  ）

           A．200件          B．5000件        C．2500件             D．1000件

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设点列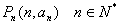，数列{an}的前n项和为Sn, 且Sn = 2n2 + 3n ， 则直线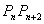的一个方向向量的坐标可以是…………………………………………… （    ）

    A．（2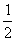，）     B．(-1, -1)    C．（）      D． (, -1)

    查看答案和解析>>

    同步练习册答案