
分析 (1)求出函数的零点,得到数列的第一项与第三项,求出公差,然后求解通项公式.
(2)利用错位相减法求解数列的或即可.
解答 解:(1)函数f(x)=x2-10x+21的两个零点为3,7,
由题意得a1=3,a3=7.
设数列的公差为:d,则2d=4,d=2,数列{an}的通项公式:an=2n+1.
(2)bn=an×3n=(2n+1)×3n,可得${S_n}=3×3+5×{3^2}+…+({2n-1})×{3^{n-1}}+({2n+1})×{3^n}$,$3{S_n}=3×{3^2}+5×{3^3}+…+({2n-1})×{3^n}+({2n+1})×{3^{n+1}}$,
两式相减得$-2{S_n}=9+2×({{3^2}+{3^3}+…+{3^n}})-({2n+1})×{3^{n+1}}=9+({{3^{n+1}}-9})-({2n+1})×{3^{n+1}}$,
所以${S_n}=n×{3^{n+1}}$.
点评 本题考查数列的通项公式以及数列求和,考查计算能力以及转化思想的应用.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
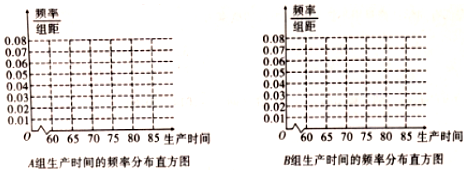
| 生产时间 | [60,65) | [65,70) | [70,75) | [75,80) |
| 人数 | 30 | 40 | 20 | 10 |
| 生产时间 | [60,65) | [65,70) | [70,75) | [75,80) | [80,85) |
| 人数 | 10 | 25 | 20 | 30 | 15 |
| 生产时间小于70分钟 | 生产时间不小于70分钟 | 合计 | |
| A组工人 | a= | b= | |
| B组工人 | c= | d= | |
| 合计 | n= |
| P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.025 | 0.01 | 0.005 | 0.001 |
| k0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2$\sqrt{2}$ | B. | 2$\sqrt{2}$ | C. | -$\sqrt{2}$ | D. | $\sqrt{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com