
 ,对任意
,对任意 ,试判断
,试判断 的形状;
的形状; 中,
中, ,
, 为
为 的中点,
的中点, 交
交 于
于 ,求证:
,求证: .
.
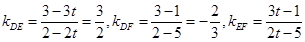 …………3分
…………3分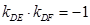 ∴
∴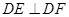
 是直角三角形………………………………………………………6分
是直角三角形………………………………………………………6分 为原点,
为原点, 所在直线为
所在直线为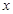 轴建立平面直角坐标系,则
轴建立平面直角坐标系,则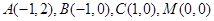 ,
,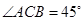 ……………………………8分
……………………………8分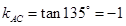 ,直线
,直线 的方程为
的方程为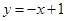 ……………………9分
……………………9分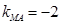 ,直线
,直线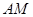 的方程为
的方程为 ,…………………………………10分
,…………………………………10分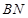 的方程为
的方程为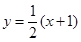 ……………………………………11分
……………………………………11分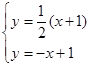 ,解得
,解得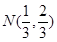 ……………………………12分
……………………………12分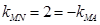 即
即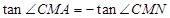 ………………………13分
………………………13分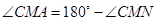 又
又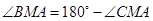
 …………………………………………………14分
…………………………………………………14分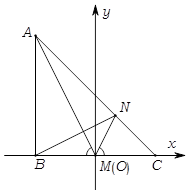
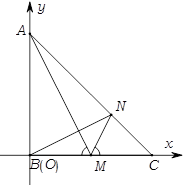
 为原点,
为原点, 所在直线为
所在直线为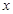 轴建立平面直角坐标系,则
轴建立平面直角坐标系,则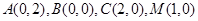 ,
,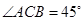 ……………………8分
……………………8分 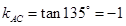 ,直线
,直线 的方程为
的方程为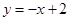 …………………9分
…………………9分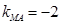 ,直线
,直线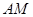 的方程为
的方程为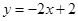 ,…………………………10分
,…………………………10分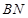 的方程为
的方程为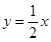 …………………………………………………11分
…………………………………………………11分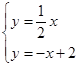 ,解得
,解得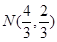 ………………………………12分
………………………………12分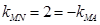 即
即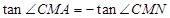 …………………………13分
…………………………13分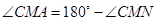
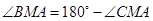
 ………………………………………………………14分
………………………………………………………14分

 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源:不详 题型:解答题
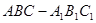 的直观图及三视图(主视图和俯视图是正方形,左侧图是等腰直角三角形)如图,
的直观图及三视图(主视图和俯视图是正方形,左侧图是等腰直角三角形)如图,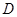 为
为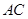 的中点.
的中点.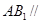 平面
平面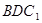 ;
;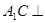 平面
平面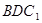 ;
; 的正切值.
的正切值.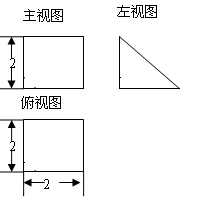
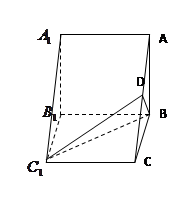
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.①② | B.③④ | C.②③ | D.②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com