
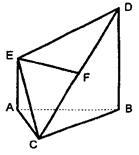
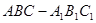 的直观图及三视图(主视图和俯视图是正方形,左侧图是等腰直角三角形)如图,
的直观图及三视图(主视图和俯视图是正方形,左侧图是等腰直角三角形)如图,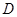 为
为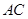 的中点.
的中点.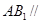 平面
平面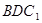 ;
;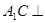 平面
平面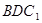 ;
;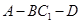 的正切值.
的正切值.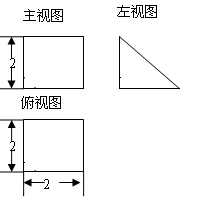
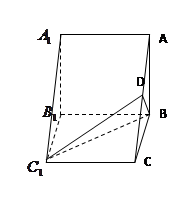
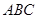 —
—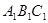 ,侧面
,侧面
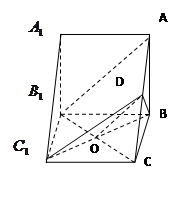
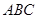 是等腰直角三角形,
是等腰直角三角形,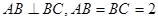 ………2分(1)连BC交
………2分(1)连BC交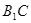 于O,连接OD,在
于O,连接OD,在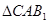 中,O,D分别是
中,O,D分别是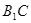 ,
,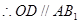
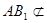 平面
平面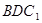 ,
,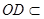 平面
平面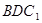 ,
,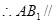 平面
平面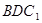 ………………..4分
………………..4分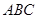 —
—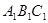 中,
中,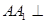 平面
平面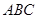 ,
,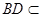 平面
平面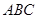 ,
,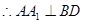 ,
,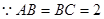 ,D为AC的中点,
,D为AC的中点,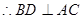 ,
,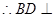 平面
平面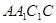 ,
,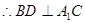 ①………………..6分
①………………..6分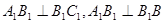 ,
,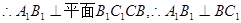
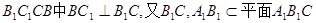
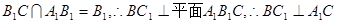 ②………………..8分
②………………..8分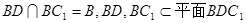 ,
, ……………………………………………………………9
……………………………………………………………9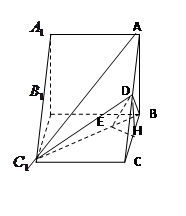 (3)解法一;提示:所求二面角与二面角C-
(3)解法一;提示:所求二面角与二面角C-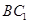 -D互余……………………………………..12
-D互余……………………………………..12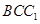 ,过H作
,过H作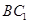 垂线,垂足为E,
垂线,垂足为E,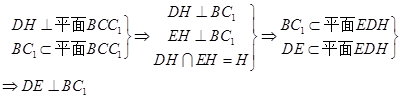
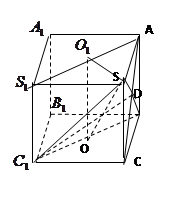 所以二面角C-
所以二面角C-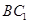 -D的平面角是∠DEH…………….. ……………………12分
-D的平面角是∠DEH…………….. ……………………12分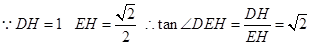 ,因为二面角A-
,因为二面角A-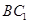 -D与二面角C-
-D与二面角C-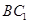 -D互余,所以二面角A-
-D互余,所以二面角A-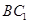 -D的正切值为
-D的正切值为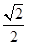 ;……………..14
;……………..14
|
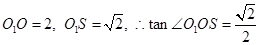 ……………..14
……………..14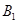 为原点建系,易得
为原点建系,易得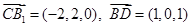
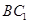 D的法向量
D的法向量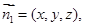 由
由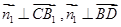
 令
令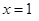 得
得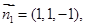 …………..12
…………..12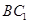 A的法向量
A的法向量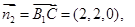
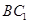 -D的平面角为
-D的平面角为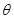
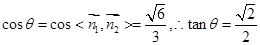 …………..14
…………..14

 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,对任意
,对任意 ,试判断
,试判断 的形状;
的形状; 中,
中, ,
, 为
为 的中点,
的中点, 交
交 于
于 ,求证:
,求证: .
.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
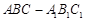 的底面是直角三角形,
的底面是直角三角形,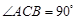 ,侧棱与底面所成角为
,侧棱与底面所成角为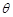 ,点
,点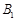 在底面上射影D落在BC上.
在底面上射影D落在BC上.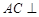 平面
平面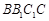 ;
;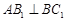 ,求
,求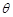 的大小;
的大小;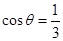 ,且当
,且当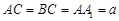 时,求二面角
时,求二面角 的大小.
的大小.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 是边长为
是边长为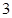 的正方形,
的正方形,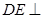 平面
平面 ,
,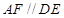 ,
,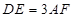 ,
,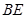 与平面
与平面 所成角为
所成角为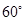 .
.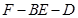 的余弦值;
的余弦值;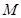 是线段
是线段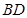 上的一个动点,问当
上的一个动点,问当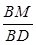 的值为多少时,可使得
的值为多少时,可使得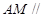 平面
平面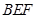 ,并证明你的结论.
,并证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com