
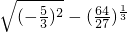 =________.
=________.科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
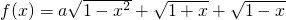 的最大值为g(a).
的最大值为g(a).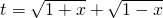 ,把函数f(x)表示为t的函数h(t),并写出定义域;
,把函数f(x)表示为t的函数h(t),并写出定义域;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 .请完成以下任务:
.请完成以下任务:| x | 0 | 0.1 | 0.2 | 0.5 | 0.8 | 1 | 1.2 | 1.5 | 1.8 | 2 | 4 | 6 | … |
| y | 0 | 0.396 | 0.769 | 1.6 | 1.951 | 2 | 1.967 | 1.846 | 1.698 | 1.6 | 0.941 | 0.649 | … |
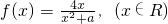 的值域.
的值域. .
.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
 ,取函数f(x)=2-|x|.当K=
,取函数f(x)=2-|x|.当K= 时,函数fK(x)的单调递减区间为
时,函数fK(x)的单调递减区间为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com