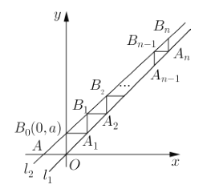
[题目]已知直线.斜率为的直线与x轴交于点A.与y轴交于点.过作x 轴的平行线.交于点.过作y轴的平行线.交于点.再过作x轴的平行线交于点.-.这样依次得线段....-...记为点的横坐标.则．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

【题目】已知直线，斜率为的直线与x轴交于点A，与y轴交于点，过作x 轴的平行线，交于点，过作y轴的平行线，交于点，再过作x轴的平行线交于点，…，这样依次得线段、、、、…、、，记为点的横坐标，则__________．

【答案】

【解析】

先由题设条件得出点的坐标，根据它们之间的关系求出点的坐标，然后利用数列极限的运算性质求出.

解：∵斜率为的直线与x轴交于点A，与y轴交于点，直线，

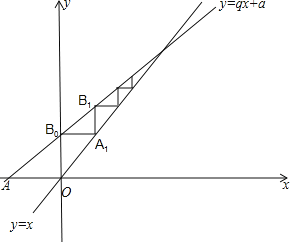
∴A1（a，a）.

∵A1B0∥x轴，∴B1（a，aq+a），A2（aq+a，aq+a）.

∵B1A2∥x轴，∴B2（aq+a，aq2+aq+a）.

同理可得：A3（aq2+aq+a，aq2+aq+a），

B3（aq2+aq+a，aq3+aq2+aq+a），…，

Bn（aqn﹣1+aqn﹣2+aqn﹣3+…aq2+aq+a，aqn+aqn﹣1+aqn﹣2+aqn﹣3+…aq2+aq+a），

∵xn为点Bn的横坐标，

∴xn＝aqn﹣1+aqn﹣2+aqn﹣3+…aq2+aq+a.

故xn是首项为a，公比为q（0＜q＜1）的等比数列的前n项的和，

由数列极限的运算性质得：.

故答案为：.

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：

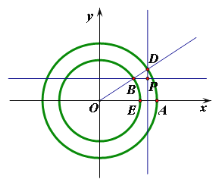
【题目】已知圆，圆，如图，分别交轴正半轴于点.射线分别交于点，动点满足直线与轴垂直，直线与轴垂直.

（1）求动点的轨迹的方程；

（2）过点作直线交曲线与点，射线与点，且交曲线于点.问：的值是否是定值？如果是定值，请求出该定值；如果不是定值，请说明理由.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】在某外国语学校举行的(高中生数学建模大赛)中,参与大赛的女生与男生人数之比为,且成绩分布在,分数在以上(含)的同学获奖．按女生、男生用分层抽样的方法抽取人的成绩作为样本,得到成绩的频率分布直方图如图所示．

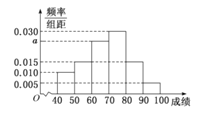
(Ⅰ)求的值,并计算所抽取样本的平均值(同一组中的数据用该组区间的中点值作代表)；

(Ⅱ)填写下面的列联表,并判断在犯错误的概率不超过的前提下能否认为“获奖与女生、男生有关”．

	女生	男生	总计
获奖
不获奖
总计

附表及公式：

其中,．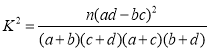

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如图，抛物线的焦点为，过点作直线与抛物线交于、两点，当直线与轴垂直时长为.

（1）求抛物线的方程；

（2）若与的面积相等，求直线的方程.

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】已知函数．

（1）求在处的切线方程：

（2）已知实数时，求证：函数的图象与直线：有3个交点．

查看答案和解析>>

科目：高中数学 来源： 题型：

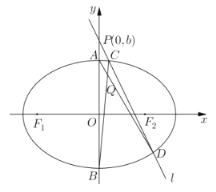
【题目】在平面直角坐标系中，A、B分别为椭圆的上、下顶点，若动直线l过点，且与椭圆相交于C、D两个不同点（直线l与y轴不重合，且C、D两点在y轴右侧，C在D的上方），直线AD与BC相交于点Q．

（1）设的两焦点为、，求的值;

（2）若，且，求点Q的横坐标；

（3）是否存在这样的点P，使得点Q的纵坐标恒为？若存在，求出点P的坐标，若不存在，请说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：

【题目】如下为简化的计划生育模型：每个家庭允许生男孩最多一个，即某一胎若为男孩，则不能再生下一胎，而女孩可以多个.为方便起见，此处约定每个家庭最多可生育3个小孩，即若第一胎或前两胎为女孩，则继续生，但若第三胎还是女孩，则不能再生了.设每一胎生男生女等可能，且各次生育相互独立.依据每个家庭最多生育一个男孩的政策以及我们对生育女孩的约定，令为某一家庭所生的女孩数，为此家庭所生的男孩数.