
【题目】已知函数![]() .
.
(1)求![]() 在
在![]() 处的切线方程:
处的切线方程:
(2)已知实数![]() 时,求证:函数
时,求证:函数![]() 的图象与直线
的图象与直线![]() :
:![]() 有3个交点.
有3个交点.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)求出原函数的导函数,可得![]() ,再求出切点为(1,0),利用直线方程的点斜式可得函数的图象在
,再求出切点为(1,0),利用直线方程的点斜式可得函数的图象在![]() 处的切线方程;
处的切线方程;
(2)函数![]() 的图象与直线
的图象与直线![]() 交点的个数等价于函数
交点的个数等价于函数![]() 的零点个数,通过导数判断函数的单调性,求函数的最值同0进行比较,得到结果.
的零点个数,通过导数判断函数的单调性,求函数的最值同0进行比较,得到结果.
(1)因为![]() ,所以
,所以![]() ,
,
所以![]() ,
,
又因为![]() ,所以
,所以![]() 在
在![]() 处的切线方程
处的切线方程![]() ;
;
(2)证明:当![]() 时,函数
时,函数![]() 的图象与直线
的图象与直线![]() 交点的个数等价于函数
交点的个数等价于函数![]() 的零点个数,
的零点个数,
因为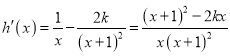 ,
,![]() ,
,
设![]() ,
,
因为二次函数![]() 在
在![]() 时,
时,![]() ,
,![]() ,
,
所以存在![]() ,
,![]() ,使得
,使得![]() ,
,![]() ,
,
所以![]() 在
在![]() 单调递增,
单调递增,![]() 单调递减,
单调递减,![]() 单调递增.
单调递增.
因为![]() ,所以
,所以![]() ,
,![]() ,
,
因此![]() 在
在![]() 存在一个零点
存在一个零点![]() ;
;
又因为当![]() ,
,![]() ,
,
所以![]() 在
在![]() 存在一个零点;
存在一个零点;
当![]() 时,
时,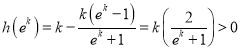 ,
,
所以![]() 在
在![]() 存在一个零点;
存在一个零点;
所以,函数![]() 的图象与直线
的图象与直线![]() :
:![]() 有3个交点.
有3个交点.


科目:高中数学 来源: 题型:
【题目】定义行列式的运算如下: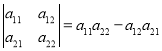 ,已函数
,已函数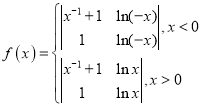 以下命题正确的是( )
以下命题正确的是( )
①对![]() ,都有
,都有![]() ;②若
;②若![]() ,对
,对![]() ,总存在非零常数了,使得
,总存在非零常数了,使得![]() ;③若存在直线
;③若存在直线![]() 与
与![]() 的图象无公共点,且使
的图象无公共点,且使![]() 的图案位于直线两侧,此直线即称为函数
的图案位于直线两侧,此直线即称为函数![]() 的分界线.则
的分界线.则![]() 的分界线的斜率的取值范围是
的分界线的斜率的取值范围是![]() ;④函数
;④函数![]() 的零点有无数个.
的零点有无数个.
A.①③④B.①②④
C.②③D.①④
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P—ABCD中,底面ABCD是菱形,PC⊥BC,点E是PC的中点,且平面PBC⊥平面ABCD.求证:
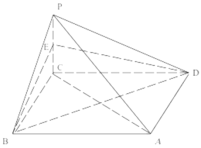
(1)求证:PA∥平面BDE;
(2)求证:平面PAC⊥平面BDE.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国在欧洲的某孔子学院为了让更多的人了解中国传统文化,在当地举办了一场由当地人参加的中国传统文化知识大赛,为了了解参加本次大赛参赛人员的成绩情况,从参赛的人员中随机抽取![]() 名人员的成绩(满分100分)作为样本,将所得数据进行分析整理后画出频率分布直方图如图所示,已知抽取的人员中成绩在[50,60)内的频数为3.
名人员的成绩(满分100分)作为样本,将所得数据进行分析整理后画出频率分布直方图如图所示,已知抽取的人员中成绩在[50,60)内的频数为3.
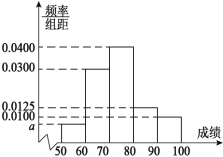
(1)求![]() 的值和估计参赛人员的平均成绩(保留小数点后两位有效数字);
的值和估计参赛人员的平均成绩(保留小数点后两位有效数字);
(2)已知抽取的![]() 名参赛人员中,成绩在[80,90)和[90,100]女士人数都为2人,现从成绩在[80,90)和[90,100]的抽取的人员中各随机抽取2人,记这4人中女士的人数为
名参赛人员中,成绩在[80,90)和[90,100]女士人数都为2人,现从成绩在[80,90)和[90,100]的抽取的人员中各随机抽取2人,记这4人中女士的人数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
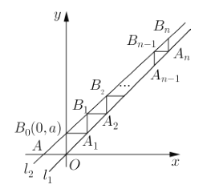
【题目】已知直线![]() ,斜率为
,斜率为![]() 的直线
的直线![]() 与x轴交于点A,与y轴交于点
与x轴交于点A,与y轴交于点![]() ,过
,过![]() 作x 轴的平行线,交
作x 轴的平行线,交![]() 于点
于点![]() ,过
,过![]() 作y轴的平行线,交
作y轴的平行线,交![]() 于点
于点![]() ,再过
,再过![]() 作x轴的平行线交
作x轴的平行线交![]() 于点
于点![]() ,…,这样依次得线段
,…,这样依次得线段![]() 、
、![]() 、
、![]() 、
、![]() 、…、
、…、![]() 、
、![]() ,记
,记![]() 为点
为点![]() 的横坐标,则
的横坐标,则![]() __________.
__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() (其中
(其中![]() ,点P的轨迹记为曲线
,点P的轨迹记为曲线![]() ,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点Q在曲线
,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,点Q在曲线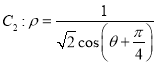 上.
上.
(1)求曲线![]() 的极坐标方程和曲线
的极坐标方程和曲线![]() 的直角坐标方程;
的直角坐标方程;
(2)当![]() ,
,![]() 时,求曲线
时,求曲线![]() 与曲线
与曲线![]() 的公共点的极坐标
的公共点的极坐标
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某外卖平台为提高外卖配送效率,针对外卖配送业务提出了两种新的配送方案,为比较两种配送方案的效率,共选取50名外卖骑手,并将他们随机分成两组,每组25人,第一组骑手用甲配送方案,第二组骑手用乙配送方案.根据骑手在相同时间内完成配送订单的数量(单位:单)绘制了如下茎叶图:
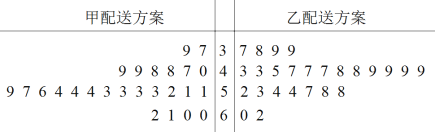
(1)根据茎叶图,求各组内25位骑手完成订单数的中位数,已知用甲配送方案的25位骑手完成订单数的平均数为52,结合中位数与平均数判断哪种配送方案的效率更高,并说明理由;
(2)设所有50名骑手在相同时间内完成订单数的平均数![]() ,将完成订单数超过
,将完成订单数超过![]() 记为“优秀”,不超过
记为“优秀”,不超过![]() 记为“一般”,然后将骑手的对应人数填入下面列联表;
记为“一般”,然后将骑手的对应人数填入下面列联表;
优秀 | 一般 | |
甲配送方案 | ||
乙配送方案 |
(3)根据(2)中的列联表,判断能否有![]() 的把握认为两种配送方案的效率有差异.
的把握认为两种配送方案的效率有差异.
附: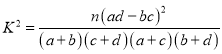 ,其中
,其中![]() .
.
| 0.05 | 0.010 | 0.005 |
| 3.841 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() ,过
,过![]() 的直线与抛物线
的直线与抛物线![]() 相交于
相交于![]() 两点.
两点.
(1)若点![]() 是点
是点![]() 关于坐标原点
关于坐标原点![]() 的对称点,求
的对称点,求![]() 面积的最小值;
面积的最小值;
(2)是否存在垂直于![]() 轴的直线
轴的直线![]() ,使得
,使得![]() 被以
被以![]() 为直径的圆截得的弦长恒为定值?若存在,求出
为直径的圆截得的弦长恒为定值?若存在,求出![]() 的方程和定值;若不存在,说明理由.
的方程和定值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com