练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

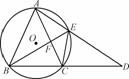
    如图，圆O是等腰三角形ABC的外接圆，AB＝AC，延长BC到点D，使CD＝AC，连结AD交圆O于点E，连结BE与AC交于点F.

    (1) 判断BE是否平分∠ABC，并说明理由；

    (2) 若AE＝6，BE＝8，求EF的长．


    解：(1) BE平分∠ABC.

    ∵ CD＝AC，∴ ∠D＝∠CAD.

    ∵ AB＝AC，∴ ∠ABC＝∠ACB.

    ∵ ∠EBC＝∠CAD，∴ ∠EBC＝∠D＝∠CAD.

    ∵ ∠ABC＝∠ABE＋∠EBC，∠ACB＝∠D＋∠CAD，

    ∴ ∠ABE＝∠EBC，即BE平分∠ABC.

    (2) 由(1)知∠CAD＝∠EBC＝∠ABE.

    ∵ ∠AFE＝∠ABE，

    ∴ △AEF∽△BEA.∴ ＝.

    ∵ AE＝6，BE＝8，

    ∴ EF＝＝＝.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    设曲线2x2＋2xy＋y2＝1在矩阵A＝ (a>0)对应的变换作用下得到的曲线为x2＋y2＝1.

    (1) 求实数a、b的值；

    (2) 求A2的逆矩阵．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在极坐标系中，已知曲线C1：ρ＝12sinθ，曲线C2：ρ＝12cos.

    (1) 求曲线C1和C2的直角坐标方程；

    (2) 若P、Q分别是曲线C1和C2上的动点，求PQ的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    在直角三角形ABC中，点D是斜边AB的中点，点P为线段CD的中点，求.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，点B在圆O上， M为直径AC上一点，BM的延长线交圆O于N，∠BNA＝45°，若圆O的半径为2 ，OA＝OM，求MN的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，AB是圆O的直径，点C在圆O上，延长BC到D使BC＝CD，过C作圆O的切线交AD于E.若AB＝6，ED＝2，求BC的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


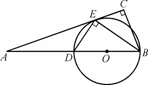
    如图，在△ABC中，∠C＝90°，BE是角平分线，DE⊥BE交AB于D，圆O是△BDE的外接圆．

    (1) 求证：AC是圆O的切线；

    (2) 如果AD＝6，AE＝6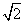，求BC的长．

     

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若不等式|3x－b|＜4的解集中整数有且只有1，2，3，求实数b的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝ln x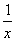＋－1.

    (1)求函数f(x)的单调区间；

    (2)设m∈R，对任意的a∈(－1,1)，总存在x0∈[1，e]，使得不等式ma－f(x0)＜0成立，求实数m的取值范围．

    查看答案和解析>>

    同步练习册答案