练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

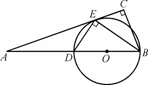
    如图，在△ABC中，∠C＝90°，BE是角平分线，DE⊥BE交AB于D，圆O是△BDE的外接圆．

    (1) 求证：AC是圆O的切线；

    (2) 如果AD＝6，AE＝6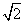，求BC的长．

     


     (1) 证明：连OE，∵BE⊥DE，

    ∴O点为BD的中点．

    ∵OB＝OE，∴∠OEB＝∠OBE.

    ∵∠OEC＝∠OEB＋∠CEB＝∠OBE＋∠CEB＝∠CEB＋∠CBE＝90°，即OE⊥AC.

    又E是AC与圆O的公共点，∴AC是圆O的切线．

    (2) 解：∵AE是圆的切线，∴∠AED＝∠ABE.

    又∠A共用，∴△ADE∽△AEB，

    ∴解得AB＝12，

    ∴圆O的半径为3.

    又∵OE∥BC，∴解得BC＝4.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知直线l经过点P(1，1)，倾斜角α＝.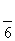

    (1) 写出直线l的参数方程；

    (2) 设l与圆x2＋y2＝4相交于两点A、B，求点P到A、B两点的距离之积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


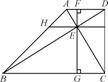
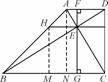
    如图，在梯形ABCD中，AD∥BC，AC⊥BD，垂足为E，∠ABC＝45°，过E作AD的垂线交AD于F，交BC于G，过E作AD的平行线交AB于H.求证：FG2＝AF·DF＋BG·CG＋AH·BH.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


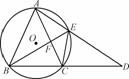
    如图，圆O是等腰三角形ABC的外接圆，AB＝AC，延长BC到点D，使CD＝AC，连结AD交圆O于点E，连结BE与AC交于点F.

    (1) 判断BE是否平分∠ABC，并说明理由；

    (2) 若AE＝6，BE＝8，求EF的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，AB和BC分别与圆O相切于点D、C，AC经过圆心O，且BC＝2OC.求证：AC＝2AD.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    求函数y＝|x－4|＋|x－6|的最小值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若关于实数x的不等式|x－5|＋|x＋3|<a无解，求实数a的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}满足an＋1＝an－an－1(n≥2)，a1＝1，a2＝3，记Sn＝a1＋a2＋…＋an，则下列结论正确的是(　　)

    A．a100＝－1，S100＝5               B．a100＝－3，S100＝5

    C．a100＝－3，S100＝2               D．a100＝－1，S100＝2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数①f(x)＝x2；②f(x)＝ex；③f(x)＝ln x；④f(x)＝cos x．其中对于f(x)定义域内的任意一个x1都存在唯一的x2，使f(x1)f(x2)＝1成立的函数是(　　)

    A．①                           B．②

    C．②③                         D．③④

    查看答案和解析>>

    同步练习册答案