练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝ln x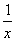＋－1.

    (1)求函数f(x)的单调区间；

    (2)设m∈R，对任意的a∈(－1,1)，总存在x0∈[1，e]，使得不等式ma－f(x0)＜0成立，求实数m的取值范围．


    解析：　(1)f′(x)＝，x＞0.

    令f′(x)＞0，得x＞1，因此函数f(x)的单调递增区间是(1，＋∞)．

    令f′(x)＜0，得0＜x＜1，因此函数f(x)的单调递减区间是(0,1)．

    (2)依题意，ma＜f(x)max.

    由(1)知，f(x)在x∈[1，e]上是增函数，

    ∴f(x)max＝f(e)＝ln e＋－1＝.

    ∴ma＜，即ma－＜0对于任意的a∈(－1,1)恒成立．

    ∴解得－≤m≤.

    ∴m的取值范围是.


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


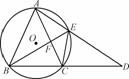
    如图，圆O是等腰三角形ABC的外接圆，AB＝AC，延长BC到点D，使CD＝AC，连结AD交圆O于点E，连结BE与AC交于点F.

    (1) 判断BE是否平分∠ABC，并说明理由；

    (2) 若AE＝6，BE＝8，求EF的长．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知数列{an}满足an＋1＝an－an－1(n≥2)，a1＝1，a2＝3，记Sn＝a1＋a2＋…＋an，则下列结论正确的是(　　)

    A．a100＝－1，S100＝5               B．a100＝－3，S100＝5

    C．a100＝－3，S100＝2               D．a100＝－1，S100＝2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设z＝x＋y，其中实数x，y满足若z的最大值为6，则z的最小值为(　　)

    A．－3                            B．－2

    C．－1                            D．0

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    设函数f(x)＝ax＋b(0≤x≤1)，则a＋2b＞0是f(x)＞0在[0,1]上恒成立的________条件．(填充分但不必要，必要但不充分，充要，既不充分也不必要)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    如图，在边长为a的正方形内有不规则图形Ω.向正方形内随机撒豆子，若撒在图形Ω内和正方形内的豆子数分别为m，n，则图形Ω面积的估计值为(　　)

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数①f(x)＝x2；②f(x)＝ex；③f(x)＝ln x；④f(x)＝cos x．其中对于f(x)定义域内的任意一个x1都存在唯一的x2，使f(x1)f(x2)＝1成立的函数是(　　)

    A．①                           B．②

    C．②③                         D．③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若点P(1,1)是圆x2＋(y－3)2＝9的弦AB的中点，则直线AB的方程为(　　)

    A．x－2y＋1＝0                  B．x＋2y－3＝0

    C．2x＋y－3＝0                  D．2x－y－1＝0

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    某中学有4位学生申请A，B，C三所大学的自主招生．若每位学生只能申请其中一所大学，且申请其中任何一所大学是等可能的．

    （1）求恰有2人申请A大学的概率；

    （2）求被申请大学的个数X的概率分布列与数学期望E(X)．

    查看答案和解析>>

    同步练习册答案