考点:直线与平面所成的角,空间中直线与直线之间的位置关系
专题:空间位置关系与距离,空间角
分析:(Ⅰ)连结BC1,B1C,由正方形性质得B1C⊥BC1,由线面垂直得BC1⊥DC,所以BC1⊥平面DCB1,由AD1∥BC1,得AD1⊥平面DCB1,由此能证明EB1⊥AD1.
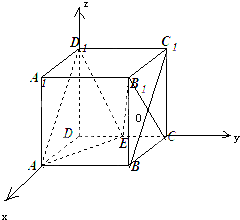
(Ⅱ)以D为原点,建立空间直角坐标系D-xyz,利用向量法能求出EB1与平面AD1E所成的角.
解答:
(Ⅰ)证明:连结BC
1,B
1C,交于点O,
∵BCC
1B
1是正方形,∴B
1C⊥BC
1,
又DC⊥平面BCC
1B
1,∴BC
1⊥DC,
∵DC∩B
1C=C,
∴BC
1⊥平面DCB
1,
∵AD
1∥BC
1,∴AD
1⊥平面DCB
1,
∵EB
1?平面DCB
1,∴EB
1⊥AD
1.
(Ⅱ)解:以D为原点,建立空间直角坐标系D-xyz,
设正方体ABCD-A
1B
1C
1D
1的棱长为2,E是CD中点,
则A(2,0,0),D
1(0,0,2),
E(0,1,0),B
1(2,2,2),
=(-2,0,2),
=(-2,1,0),
=(2,1,2),
设平面AD
1E的法向量
=(x,y,z),
则
,取x=1,得
=(1,2,1),
设EB
1与平面AD
1E所成的角为θ,
则sinθ=|cos<
,>|=|
|=
.
∴EB
1与平面AD
1E所成的角为arcsin
.
点评:本题考查异面直线垂直的证明,考查直线与平面所成角的大小的求法,解题时要认真审题,注意向量法的合理运用.

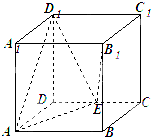 正方体ABCD-A1B1C1D1中,点E在棱CD上.
正方体ABCD-A1B1C1D1中,点E在棱CD上.


 步步高达标卷系列答案
步步高达标卷系列答案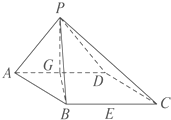 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°.侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD边的中点.
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°.侧面PAD为正三角形,其所在的平面垂直于底面ABCD,G为AD边的中点. 有一海湾,海岸线近似为椭圆的一段弧NM,M、N为椭圆弧上两点,且MA⊥AB,NB⊥AB,AB间的距离为2公里,椭圆焦点为A、B,椭圆的短半轴长为
有一海湾,海岸线近似为椭圆的一段弧NM,M、N为椭圆弧上两点,且MA⊥AB,NB⊥AB,AB间的距离为2公里,椭圆焦点为A、B,椭圆的短半轴长为 如图所示,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,AB=1,BC=
如图所示,在直四棱柱ABCD-A1B1C1D1中,底面ABCD是矩形,AB=1,BC=