
已知函数 (
( ).
).
(1)若 ,求函数
,求函数 的极值;
的极值;
(2)设 .
.
① 当 时,对任意
时,对任意 ,都有
,都有 成立,求
成立,求 的最大值;
的最大值;
② 设 的导函数.若存在
的导函数.若存在 ,使
,使 成立,求
成立,求 的取值范围.
的取值范围.
(1)参考解析; (2)①-1-e-1,②(-1,+∞)
【解析】
试题分析:(1)由函数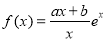 (
( ),且
),且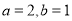 ,所以对函数
,所以对函数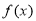 求导,根据导函数的正负性可得到结论
求导,根据导函数的正负性可得到结论
(2)①当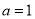 时,对任意
时,对任意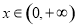 ,都有
,都有 成立,即
成立,即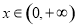 时,
时, 恒成立. 由此可以通过分离变量或直接求函数的最值求得结果,有分离变量可得b≤x2-2x-
恒成立. 由此可以通过分离变量或直接求函数的最值求得结果,有分离变量可得b≤x2-2x-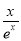 在x∈(0,+∞)上恒成立.通过求函数h(x)=x2-2x-
在x∈(0,+∞)上恒成立.通过求函数h(x)=x2-2x-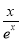 (x>0)的最小值即可得到结论.
(x>0)的最小值即可得到结论.
②若存在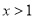 ,使
,使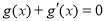 .通过表示
.通过表示 即可得到
即可得到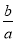 =
=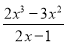 ,所以求出函数u(x)=
,所以求出函数u(x)=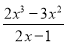 (x>1)的单调性即可得到结论.
(x>1)的单调性即可得到结论.
(1)当a=2,b=1时,f (x)=(2+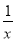 )ex,定义域为(-∞,0)∪(0,+∞).
)ex,定义域为(-∞,0)∪(0,+∞).
所以f ′(x)=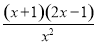 ex. 2分
ex. 2分
令f ′(x)=0,得x1=-1,x2=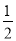 ,列表
,列表
x | (-∞,-1) | -1 | (-1,0) | (0, |
| ( |
f ′(x) |
|
| - | - |
|
|
f (x) | ↗ | 极大值 | ↘ | ↘ | 极小值 | ↗ |
由表知f (x)的极大值是f (-1)=e-1,f (x)的极小值是f ( )=4
)=4 . 4分
. 4分
(2)① 因为g (x)=(ax-a)ex-f (x)=(ax-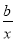 -2a)ex,
-2a)ex,
当a=1时,g (x)=(x-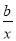 -2)ex.
-2)ex.
因为g (x)≥1在x∈(0,+∞)上恒成立,
所以b≤x2-2x-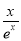 在x∈(0,+∞)上恒成立. 7分
在x∈(0,+∞)上恒成立. 7分
记h(x)=x2-2x- (x>0),则h′(x)=
(x>0),则h′(x)=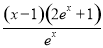 .
.
当0<x<1时,h′(x)<0,h(x)在(0,1)上是减函数;
当x>1时,h′(x)>0,h(x)在(1,+∞)上是增函数;
所以h(x)min=h(1)=-1-e-1;
所以b的最大值为-1-e-1. 9分
解法二:因为g (x)=(ax-a)ex-f (x)=(ax- -2a)ex,
-2a)ex,
当a=1时,g (x)=(x-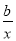 -2)ex.
-2)ex.
因为g (x)≥1在x∈(0,+∞)上恒成立,
所以g(2)=- e2>0,因此b<0. 5分
e2>0,因此b<0. 5分
g′(x)=(1+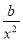 )ex+(x-
)ex+(x-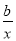 -2)ex=
-2)ex=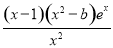 .
.
因为b<0,所以:当0<x<1时,g′(x)<0,g(x)在(0,1)上是减函数;当x>1时,g′(x)>0,g(x)在(1,+∞)上是增函数.所以g(x)min=g(1)=(-1-b)e-1 7分
因为g (x)≥1在x∈(0,+∞)上恒成立,
所以(-1-b)e-1≥1,解得b≤-1-e-1
因此b的最大值为-1-e-1. 9分
②解法一:因为g (x)=(ax- -2a)ex,所以g ′(x)=(
-2a)ex,所以g ′(x)=( +ax-
+ax-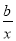 -a)ex.
-a)ex.
由g (x)+g ′(x)=0,得(ax-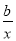 -2a)ex+(
-2a)ex+(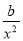 +ax-
+ax-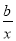 -a)ex=0,
-a)ex=0,
整理得2ax3-3ax2-2bx+b=0.
存在x>1,使g (x)+g ′(x)=0成立.
等价于存在x>1,2ax3-3ax2-2bx+b=0成立. 11分
因为a>0,所以 =
=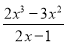 .
.
设u(x)=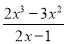 (x>1),则u′(x)=
(x>1),则u′(x)= .
.
因为x>1,u′(x)>0恒成立,所以u(x)在(1,+∞)是增函数,所以u(x)>u(1)=-1,
所以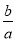 >-1,即
>-1,即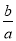 的取值范围为(-1,+∞). 14分
的取值范围为(-1,+∞). 14分
解法二:因为g (x)=(ax-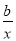 -2a)ex,所以g ′(x)=(
-2a)ex,所以g ′(x)=(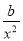 +ax-
+ax-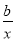 -a)ex.
-a)ex.
由g (x)+g ′(x)=0,得(ax-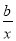 -2a)ex+(
-2a)ex+(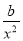 +ax-
+ax-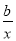 -a)ex=0,
-a)ex=0,
整理得2ax3-3ax2-2bx+b=0.
存在x>1,使g (x)+g ′(x)=0成立.
等价于存在x>1,2ax3-3ax2-2bx+b=0成立. 11分
设u(x)=2ax3-3ax2-2bx+b(x≥1)
u′(x)=6ax2-6ax-2b=6ax(x-1)-2b≥-2b 当b≤0时,u′(x)≥0
此时u(x)在[1,+∞)上单调递增,因此u(x)≥u(1)=-a-b
因为存在x>1,2ax3-3ax2-2bx+b=0成立
所以只要-a-b<0即可,此时-1<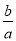 ≤0 12分
≤0 12分
当b>0时,令x0=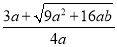 >
>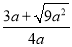 =
=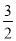 >1,得u(x0)=b>0,
>1,得u(x0)=b>0,
又u(1)=-a-b<0于是u(x)=0,在(1,x0)上必有零点
即存在x>1,2ax3-3ax2-2bx+b=0成立,此时 >0 13分
>0 13分
综上有 的取值范围为(-1,+∞)------14分
的取值范围为(-1,+∞)------14分
考点:1.函数的极值.2.函数最值.3.函数恒成立问题.4.存在性的问题.5.运算能力.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2013-2014学年福建省龙岩市高三上学期期末考试文科数学试卷(解析版) 题型:选择题
设变量x,y满足约束条件 ,则目标函数z=2y-3x的最大值为( )
,则目标函数z=2y-3x的最大值为( )
A. -3 B. 2 C. 4 D. 5
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高三高考压轴文科数学试卷(解析版) 题型:选择题
已知直线 经过坐标原点,且与圆
经过坐标原点,且与圆 相切,切点在第四象限,则直线
相切,切点在第四象限,则直线 的方程为( )
的方程为( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省福州市高三5月综合练习理科数学试卷(解析版) 题型:填空题
在△ABC中,AB=2,D为BC的中点,若 =
=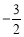 ,则AC=_____ __.
,则AC=_____ __.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省福州市高三5月综合练习理科数学试卷(解析版) 题型:选择题
已知 ,n∈N※,如果执行右边的程序框图,那么输出的
,n∈N※,如果执行右边的程序框图,那么输出的 等于( )
等于( )
A.18.5 B.37 C.185 D.370

查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省福州市高三5月综合练习文科数学试卷(解析版) 题型:解答题
已知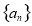 是一个公差大于0的等差数列,且满足
是一个公差大于0的等差数列,且满足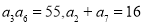 .
.
(1)求数列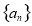 的通项公式;
的通项公式;
(2)若数列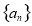 和数列
和数列 满足等式:
满足等式: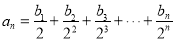 (n为正整数)求数列
(n为正整数)求数列 的前n项和
的前n项和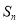 .
.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省福州市高三5月综合练习文科数学试卷(解析版) 题型:选择题
已知P(x,y)为椭圆 上一点,F为椭圆C的右焦点,若点M满足
上一点,F为椭圆C的右焦点,若点M满足 且
且 ,则
,则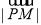 的最小值为( )
的最小值为( )
A. B.3 C.
B.3 C. D.1
D.1
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高考考前模拟理科数学试卷(解析版) 题型:解答题
某同学用“五点法”画函数 在某一个周期内的图象时,列表并填入的部分数据如下表:
在某一个周期内的图象时,列表并填入的部分数据如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请求出上表中的 ,并直接写出函数
,并直接写出函数 的解析式;
的解析式;
(2)将 的图象沿
的图象沿 轴向右平移
轴向右平移 个单位得到函数
个单位得到函数 ,若函数
,若函数 在
在 (其中
(其中 )上的值域为
)上的值域为 ,且此时其图象的最高点和最低点分别为
,且此时其图象的最高点和最低点分别为 ,求
,求 与
与 夹角
夹角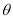 的大小。
的大小。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com