
某同学用“五点法”画函数 在某一个周期内的图象时,列表并填入的部分数据如下表:
在某一个周期内的图象时,列表并填入的部分数据如下表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(1)请求出上表中的 ,并直接写出函数
,并直接写出函数 的解析式;
的解析式;
(2)将 的图象沿
的图象沿 轴向右平移
轴向右平移 个单位得到函数
个单位得到函数 ,若函数
,若函数 在
在 (其中
(其中 )上的值域为
)上的值域为 ,且此时其图象的最高点和最低点分别为
,且此时其图象的最高点和最低点分别为 ,求
,求 与
与 夹角
夹角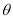 的大小。
的大小。
(1) ;(2)
;(2) .
.
【解析】
试题分析:本题主要考查五点作图法、三角函数图象的平移、三角函数值域、向量的夹角公式等基础知识,考查学生的分析问题解决问题的能力、计算能力,考查学生的数形结合思想.第一问,结合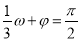 且
且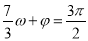 ,得出
,得出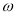 和
和 ,再解方程求出
,再解方程求出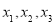 的值,再结合三角函数图象写出
的值,再结合三角函数图象写出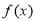 解析式;第二问,先将
解析式;第二问,先将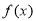 图象向右平移得到
图象向右平移得到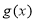 解析式,结合正弦图象,利用值域确定最高点、最低点的坐标,从而得到
解析式,结合正弦图象,利用值域确定最高点、最低点的坐标,从而得到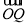 和
和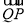 向量坐标,利用夹角公式求出
向量坐标,利用夹角公式求出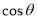 ,再确定角
,再确定角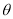 .
.
试题解析:(1) ,
,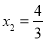 ,
,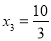 , 3分
, 3分
∴ , 5分
, 5分
(2)将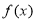 的图象沿x轴向右平移
的图象沿x轴向右平移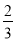 个单位得到函数
个单位得到函数 , 6分
, 6分
由于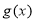 在
在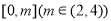 上的值域为
上的值域为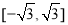 ,
,
则 ,故最高点为
,故最高点为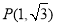 ,最近点为
,最近点为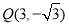 . 8分
. 8分
则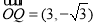 ,
, ,则
,则 ,故
,故 . 12分
. 12分
考点:五点作图法、三角函数图象的平移、三角函数值域、向量的夹角公式.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源:2013-2014学年福建省高三高考压轴文科数学试卷(解析版) 题型:解答题
已知实数 ,且
,且 按某种顺序排列成等差数列.
按某种顺序排列成等差数列.
(1)求实数 的值;
的值;
(2)若等差数列 的首项和公差都为
的首项和公差都为 ,等比数列
,等比数列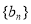 的首项和公比都为
的首项和公比都为 ,数列
,数列 和
和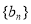 的前
的前 项和分别为
项和分别为 ,且
,且 ,求满足条件的自然数
,求满足条件的自然数 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省福州市高三5月综合练习文科数学试卷(解析版) 题型:解答题
已知函数 (
( ).
).
(1)若 ,求函数
,求函数 的极值;
的极值;
(2)设 .
.
① 当 时,对任意
时,对任意 ,都有
,都有 成立,求
成立,求 的最大值;
的最大值;
② 设 的导函数.若存在
的导函数.若存在 ,使
,使 成立,求
成立,求 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省福州市高三5月综合练习文科数学试卷(解析版) 题型:选择题
执行如图所示的程序框图,如果输出的结果为 ,则判断框内应填入的条件是( )
,则判断框内应填入的条件是( )
A.k<3 B.k>3 C.k<4 D.k>4

查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省高考考前模拟理科数学试卷(解析版) 题型:解答题
(1)设 ,若矩阵A=
,若矩阵A= 的变换把直线
的变换把直线 变换为另一直线
变换为另一直线 .
.
(1)求 的值;
的值;
(2)求矩阵A的特征值.
查看答案和解析>>
科目:高中数学 来源:2013-2014学年福建省厦门市高三5月适应性考试理科数学试卷(解析版) 题型:选择题
甲、乙、丙、丁四个人排成一行,则乙、丙位于甲的同侧的排法种数是( )
A.16 B.12 C.8 D.6
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com